الرئيسي > تزجيج > وظيفة الانتفاخ. تحدب وظيفة. اتجاه الانتفاخ. نقاط الانقلاب. شروط التحدب والانعطاف. وظيفة مؤامرة الخطوط المقاربة


وظيفة الانتفاخ. تحدب وظيفة. اتجاه الانتفاخ. نقاط الانقلاب. شروط التحدب والانعطاف. وظيفة مؤامرة الخطوط المقاربة




تحدب وظيفة

ضع في اعتبارك الوظيفة \ (y = f \ left (x \ right) ، \) التي يُفترض أنها متصلة على المقطع \ (\ left [(a، b) \ right]. \) الوظيفة \ (y = f \ يسار (س \ يمين) \) يسمى محدب لأسفل (أو ببساطة محدب) إذا كانت لأي نقطة \ ((x_1) \) و \ ((x_2) \) من \ (\ left [(a، b) \ right] \) \ إذا كانت هذه المتباينة صارمة لأي \ ((x_1) ، (x_2) \ in \ left [(a، b) \ right]، \) بحيث تكون \ ((x_1) \ ne (x_2)، \) ثم الوظيفة \ (f \ left (x \ right) \) اتصل محدب بدقة إلى أسفل

يتم تعريف دالة محدبة صاعدة بالمثل. الوظيفة \ (f \ left (x \ right) \) تسمى محدب (أو مقعر) إذا كانت المتباينة صحيحة لأي نقطة \ ((x_1) \) و \ ((x_2) \) من المقطع \ (\ يسار [(أ ، ب) \ يمين] \) كانت المتباينة صحيحة \ إذا كانت هذه المتباينة صارمة لأي \ ((x_1) ، (x_2) \ in \ left [(a، b) \ right] ، \) بحيث \ ((x_1) \ ne (x_2) ، \) ثم الوظيفة \ (f \ left (x \ right) \) تسمى محدب بدقة لأعلى على المقطع \ (\ يسار [(أ ، ب) \ يمين]. \)

التفسير الهندسي لتحدب الوظيفة

التعريفات المقدمة للدالة المحدبة لها تفسير هندسي بسيط.

بالنسبة للوظيفة ، محدب لأسفل (الشكل \ (1 \)) ، النقطة الوسطى \ (ب \) لأي وتر \ ((A_1) (A_2) \) تقع أعلى

وبالمثل ، بالنسبة للوظيفة ، محدب (الشكل \ (2 \)) ، النقطة الوسطى \ (ب \) لأي وتر \ ((A_1) (A_2) \) تقع أقلالنقطة المقابلة \ ((A_0) \) من الرسم البياني للوظيفة أو تتزامن مع هذه النقطة.

وظائف محدبة لها خاصية مرئية أخرى مرتبطة بالموقع ظل على الرسم البياني للوظيفة. الوظيفة \ (f \ left (x \ right) \) هي محدب لأسفل على المقطع \ (\ left [(a، b) \ right] \) إذا وفقط إذا كان الرسم البياني الخاص به لا يقل عن الظل المرسوم إليه في أي نقطة \ ((x_0) \) من المقطع \ (\ يسار [(أ ، ب) \ يمين] \) (صورة \ (3 \)).

وفقًا لذلك ، فإن الوظيفة \ (f \ left (x \ right) \) هي محدب على المقطع \ (\ left [(a، b) \ right] \) إذا وفقط إذا كان الرسم البياني الخاص به لا يكون أعلى من الظل المرسوم إليه في أي نقطة \ ((x_0) \) من المقطع \ (\ اليسار [(أ ، ب) \ يمين] \) (الشكل \ (4 \)). تمثل هذه الخصائص نظرية ويمكن إثباتها باستخدام تعريف تحدب الوظيفة.

شروط كافية للتحدب

دع الدالة \ (f \ left (x \ right) \) المشتق الأول \ (f "\ left (x \ right) \) موجود في المقطع \ (\ left [(a، b) \ right] ، \) والمشتق الثاني \ (f "" \ left (x \ right) \) - على الفاصل \ (\ left ((a، b) \ right). \) ثم تكون معايير التحدب الكافية التالية صحيحة:

    إذا \ (f "" \ left (x \ right) \ ge 0 \) للجميع \ (x \ in \ left ((a، b) \ right) ، \) فإن الوظيفة \ (f \ left (x \ يمين) \) محدب لأسفل على المقطع \ (\ يسار [(أ ، ب) \ يمين] ؛ \)

    إذا \ (f "" \ left (x \ right) \ le 0 \) للجميع \ (x \ in \ left ((a، b) \ right) ، \) فإن الوظيفة \ (f \ left (x \ يمين) \) محدب على المقطع \ (\ يسار [(أ ، ب) \ يمين]. \)

في تلك الحالات التي يكون فيها المشتق الثاني أكبر (أقل) من الصفر بدقة ، يقولون ، على التوالي ، حوالي التحدب الصارم لأسفل (أو أعلى ).

دعنا نثبت النظرية أعلاه في حالة دالة محدبة لأسفل. دع الدالة \ (f \ left (x \ right) \) لها مشتق ثانٍ غير سالب على الفاصل \ (\ left ((a، b) \ right): \) \ (f "" \ left (x \ right) ) \ ge 0. \) دع \ ((x_0) \) تشير إلى منتصف المقطع \ (\ left [((x_1) ، (x_2)) \ right]. \) افترض أن طول هذا المقطع هو \ (2h. \) ثم الإحداثيات \ ((x_1) \) و \ ((x_2) \) يمكن كتابتها على النحو التالي: \ [(x_1) = (x_0) - h ، \ ؛ \ ؛ (x_2) = (x_0 ) + h. \] قم بتوسيع الوظيفة \ (f \ left (x \ right) \) عند النقطة \ ((x_0) \) في سلسلة Taylor مع وجود الباقي في شكل Lagrange. نحصل على التعبيرات التالية: \ [(f \ left (((x_1)) \ right) = f \ left (((x_0) - h) \ right)) = (f \ left (((x_0)) \ right ) - f "\ left (((x_0)) \ right) h + \ frac ((f" "\ left (((\ xi _1)) \ right) (h ^ 2))) ((2},} \] \[ {f\left({{x_2}} \right) = f\left({{x_0} + h} \right) } = {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},} \] где \({x_0} - h !}
اجمع كلا من المساواة: \ [(f \ left (((x_1)) \ right) + f \ left (((x_2)) \ right)) = (2f \ left (((x_0)) \ right) + \ frac (((h ^ 2))) (2) \ left [(f "" \ left (((\ xi _1)) \ right) + f "" \ left (((\ xi _2)) \ right)) \ right].) \] بما أن \ ((\ xi _1)، (\ xi _2) \ in \ left ((a، b) \ right)، \) المشتقات الثانية في الجانب الأيمن غير سالبة. لذلك ، \ أو \ بمعنى ، وفقًا للتعريف ، الوظيفة \ (f \ left (x \ right) \) محدب لأسفل .

لاحظ أن الشرط الضروري لتحدب الوظيفة (أي ، النظرية المباشرة ، والتي ، على سبيل المثال ، من حالة التحدب إلى أسفل يتبع ذلك \ (f "" \ left (x \ right) \ ge 0 \ )) يتم استيفائه فقط لعدم المساواة غير الصارمة. في حالة التحدب الصارم ، لا يتم استيفاء الشرط الضروري بشكل عام. على سبيل المثال ، الوظيفة \ (f \ left (x \ right) = (x ^ 4) \) محدبة تمامًا للأسفل. ومع ذلك ، عند النقطة \ (x = 0 \) ، فإن مشتقها الثاني يساوي صفرًا ، أي عدم المساواة الصارمة \ (f "" \ left (x \ right) \ gt 0 \) لا تنطبق في هذه الحالة.

خصائص الوظائف المحدبة

نسرد بعض خصائص الدوال المحدبة ، بافتراض أن جميع الوظائف معرّفة ومستمرة في المقطع \ (\ left [(a، b) \ right]. \)

    إذا كانت الدالتان \ (f \) و \ (g \) محدبتان لأسفل (لأعلى) ، فإن أيًا منهما تركيبة خطية \ (af + bg، \) حيث \ (أ \) ، \ (ب \) أرقام حقيقية موجبة ، أيضًا محدبة لأسفل (لأعلى).

    إذا كانت الوظيفة \ (u = g \ left (x \ right) \) محدبة لأسفل ، وكانت الوظيفة \ (y = f \ left (u \ right) \) محدبة لأسفل وغير متناقصة ، إذن وظيفة معقدة \ (y = f \ left ((g \ left (x \ right)) \ right) \) سيكون أيضًا محدبًا لأسفل.

    إذا كانت الوظيفة \ (u = g \ left (x \ right) \) محدبة لأعلى ، وكانت الوظيفة \ (y = f \ left (u \ right) \) محدبة لأسفل وغير متزايدة ، إذن وظيفة معقدة \ (y = f \ left ((g \ left (x \ right)) \ right) \) سيكون محدبًا لأسفل.

    الحد الأقصى المحلي الدالة المحدبة التصاعدية المحددة في المقطع \ (\ left [(a، b) \ right]، \) هي في نفس الوقت أعظم قيمة في هذا الجزء.

    الحد الأدنى المحلي الوظيفة المحدبة للأسفل المحددة في المقطع \ (\ اليسار [(أ ، ب) \ اليمين] ، \) هي في نفس الوقت أصغر قيمة في هذا الجزء.

عندما نرسم الرسم البياني لوظيفة ما ، من المهم تحديد فترات التحدب ونقاط الانعطاف. إنها ، جنبًا إلى جنب مع فترات التناقص والزيادة ، ضرورية لنا لتمثيل الوظيفة بوضوح في شكل رسومي.

يتطلب فهم هذا الموضوع معرفة ماهية مشتق الوظيفة وكيفية حسابها وفقًا لترتيب معين ، بالإضافة إلى القدرة على حل أنواع مختلفة من عدم المساواة.

في بداية المقال ، يتم تحديد المفاهيم الأساسية. ثم سنبين العلاقة الموجودة بين اتجاه التحدب وقيمة المشتق الثاني في فترة زمنية معينة. بعد ذلك ، سنشير إلى الظروف التي يمكن بموجبها تحديد نقاط انعطاف الرسم البياني. سيتم توضيح جميع الاستدلالات بأمثلة على حلول المشكلات.

التعريف 1

لأسفل في فترة زمنية معينة في حالة عدم وجود الرسم البياني الخاص به أقل من المماس له في أي نقطة من هذه الفترة.

التعريف 2

وظيفة التفريق محدبةلأعلى في فترة زمنية معينة إذا كان الرسم البياني لهذه الوظيفة ليس أعلى من الظل لها في أي نقطة من هذه الفترة.

يمكن أيضًا تسمية دالة محدبة لأسفل مقعرة. يظهر كلا التعريفين بوضوح في الرسم البياني أدناه:

التعريف 3

نقطة انعطاف الوظيفةهي النقطة M (x 0 ؛ f (x 0)) ، التي يوجد عندها مماس للرسم البياني للدالة ، بشرط أن يكون المشتق موجودًا بالقرب من النقطة x 0 ، حيث يختلف الرسم البياني للوظيفة اتجاهات التحدب على الجانبين الأيمن والأيسر.

ببساطة ، نقطة الانعطاف هي مكان على الرسم البياني له ظل ، واتجاه انتفاخ المنحنى سيغير اتجاه الانتفاخ أثناء مروره عبر هذا المكان. إذا كنت لا تتذكر في ظل أي ظروف يكون وجود المماس الرأسي وغير الرأسي ممكنًا ، فإننا نوصي بتكرار القسم الموجود في ظل الرسم البياني للدالة عند نقطة ما.

يوجد أدناه رسم بياني لدالة بها عدة نقاط انعطاف مظللة باللون الأحمر. دعونا نوضح أن وجود نقاط انعطاف أمر اختياري. في الرسم البياني لدالة واحدة ، يمكن أن يكون هناك واحد ، أو اثنان ، أو عدة ، أو عدد غير محدود ، أو لا شيء.

في هذا القسم ، سنتحدث عن نظرية يمكنك من خلالها تحديد فترات التحدب على الرسم البياني لوظيفة معينة.

التعريف 4

سيكون الرسم البياني للدالة محدبًا في الاتجاه الهبوطي أو التصاعدي إذا كانت الدالة المقابلة y = f (x) لها مشتق محدود ثانٍ على الفترة المشار إليها x ، بشرط أن تكون المتباينة f "" (x) ≥ 0 x ∈ X (f "" (x) ≤ 0 x ∈ X) سيكون صحيحًا.

باستخدام هذه النظرية ، يمكن للمرء أن يجد فترات التقعر والتحدب في أي رسم بياني للدالة. للقيام بذلك ، تحتاج فقط إلى حل المتباينات f "" (x) ≥ 0 و f "" (x) ≤ 0 في مجال الوظيفة المقابلة.

دعونا نوضح أن تلك النقاط التي لا يوجد عندها المشتق الثاني ، ولكن يتم تحديد الوظيفة y = f (x) ، سيتم تضمينها في فترات التحدب والتقعر.

دعنا نلقي نظرة على مثال لمشكلة محددة كيفية تطبيق هذه النظرية بشكل صحيح.

مثال 1

شرط:الدالة y = x 3 6 - x 2 + 3 x - 1 معطاة. حدد في الفترات الزمنية التي سيكون فيها الرسم البياني للانتفاخات والتقعرات.

المحلول

مجال هذه الوظيفة هو مجموعة الأعداد الحقيقية بأكملها. لنبدأ بحساب المشتق الثاني.

y "= x 3 6 - x 2 + 3 x - 1" = x 2 2 - 2 x + 3 ⇒ y "= x 2 2 - 2 x + 3 = x - 2

نرى أن مجال المشتق الثاني يتزامن مع مجال الوظيفة نفسها. لذلك ، لتحديد فترات التحدبات ، نحتاج إلى حل المتباينات f "" (x) ≥ 0 و f "" (x) ≤ 0 .

y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x ≤ 2

لقد توصلنا إلى أن الرسم البياني للدالة المعينة سيكون له تقعر في المقطع [2 ؛ + ∞) والتحدب على القطعة (- ∞ ؛ 2].

من أجل الوضوح ، سوف نصور الرسم البياني للوظيفة ونضع علامة على الجزء المحدب عليه باللون الأزرق ، والجزء المقعر باللون الأحمر.

إجابه:الرسم البياني للدالة المعينة سيكون له تقعر في المقطع [2 ؛ + ∞) والتحدب على القطعة (- ∞ ؛ 2].

ولكن ماذا تفعل إذا كان مجال المشتق الثاني لا يتطابق مع مجال الوظيفة؟ هنا ، الملاحظة المذكورة أعلاه مفيدة لنا: تلك النقاط التي لا يوجد فيها المشتق الثاني الأخير ، سنقوم أيضًا بتضمين مقاطع التقعر والتحدب.

مثال 2

شرط:الدالة y = 8 x x - 1 معطاة. حدد الفواصل الزمنية التي سيكون للرسم البياني بها تقعر ، وفي أي منها - تحدب.

المحلول

أولًا ، دعنا نكتشف نطاق الدالة.

x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [0 ؛ 1) ∪ (1 ؛ +)

الآن نحسب المشتق الثاني:

y "= 8 xx - 1" = 8 1 2 x (x - 1) - x 1 (x - 1) 2 = - 4 x + 1 x (x - 1) 2 y "= - 4 x + 1 x (x - 1) 2 "= - 4 1 xx - 1 2 - (x + 1) xx - 1 2" x (x - 1) 4 = - 4 1 xx - 1 2 - x + 1 1 2 x ( x - 1) 2 + x 2 (x - 1) xx - 1 4 = = 2 3 x 2 + 6 x - 1 x 3 2 (x - 1) 3

مجال المشتق الثاني هو المجموعة x ∈ (0 ؛ 1) ∪ (1 ؛ + ∞). نرى أن x يساوي صفرًا سينتمي إلى مجال الدالة الأصلية ، لكن ليس إلى مجال المشتق الثاني. يجب تضمين هذه النقطة في جزء التقعر أو التحدب.

بعد ذلك ، نحتاج إلى حل المتباينات f "" (x) ≥ 0 و f "" (x) ≤ 0 في مجال الدالة المعينة. نستخدم طريقة الفواصل الزمنية لهذا: x = - 1 - 2 3 3 ≈ - 2، 1547 أو x = - 1 + 2 3 3 ≈ 0، 1547 البسط 2 (3 x 2 + 6 x - 1) x 2 3 x - 1 3 يصبح 0 والمقام هو 0 عندما x يساوي صفرًا أو واحدًا.

دعنا نضع النقاط الناتجة على الرسم البياني ونحدد علامة التعبير في جميع الفواصل الزمنية التي سيتم تضمينها في منطقة تعريف الوظيفة الأصلية. يشار إلى هذه المنطقة من خلال التظليل على الرسم البياني. إذا كانت القيمة موجبة ، ضع علامة زائد على الفترة الزمنية ، وإذا كانت سالبة ، فضع علامة على الفاصل الزمني.

بالتالي،

f "(x) ≥ 0 x ∈ [0 ؛ 1) ∪ (1 ؛ +) ⇔ × ∈ 0 ؛ - 1 + 2 3 3 ∪ (1 ؛ + ∞) و f "(x) ≤ 0 x ∈ [0 ؛ 1) ∪ (1 ؛ +) ⇔ x ∈ [- 1 + 2 3 3 ؛ واحد)

قم بتشغيل النقطة المحددة مسبقًا x = 0 واحصل على الإجابة المطلوبة. الرسم البياني الأصلي للوظيفة سيكون به انتفاخ هبوطي عند 0 ؛ - 1 + 2 3 3 ∪ (1 ؛ +) ، وما فوق - لـ x ∈ [- 1 + 2 3 3 ؛ واحد) .

لنرسم رسمًا بيانيًا ، ونضع علامة على الجزء المحدب عليه باللون الأزرق والمقعّر باللون الأحمر. يتم تمييز الخط المقارب العمودي بخط أسود منقط.

إجابه:الرسم البياني الأصلي للوظيفة سيكون به انتفاخ هبوطي عند 0 ؛ - 1 + 2 3 3 ∪ (1 ؛ +) ، وما فوق - لـ x ∈ [- 1 + 2 3 3 ؛ واحد) .

شروط انعطاف الرسم البياني للوظيفة

لنبدأ بصياغة الشرط الضروري لانقلاب الرسم البياني لبعض الوظائف.

التعريف 5

لنفترض أن لدينا دالة y = f (x) ، حيث يحتوي الرسم البياني الخاص بها على نقطة انعطاف. بالنسبة إلى x = x 0 ، يكون لها مشتق ثانٍ مستمر ، وبالتالي فإن المساواة f "" (x 0) = 0 ستثبت.

بالنظر إلى هذه الحالة ، يجب أن نبحث عن نقاط انعطاف بين تلك التي سيختفي فيها المشتق الثاني. لن يكون هذا الشرط كافياً: لن تناسبنا كل هذه النقاط.

لاحظ أيضًا أنه وفقًا للتعريف العام ، سنحتاج إلى خط مماس ، عمودي أو غير عمودي. في الممارسة العملية ، هذا يعني أنه من أجل إيجاد نقاط الانعطاف ، يجب على المرء أن يأخذ تلك التي يختفي فيها المشتق الثاني لهذه الوظيفة. لذلك ، لإيجاد حدود نقاط الانقلاب ، نحتاج إلى أخذ كل x 0 من مجال الوظيفة ، حيث lim x → x 0 - 0 f "(x) = ∞ و lim x → x 0 + 0 f" (س) = ∞. في أغلب الأحيان ، هذه هي النقاط التي يتحول عندها مقام المشتق الأول إلى 0.

الشرط الأول الكافي لوجود نقطة انعطاف للرسم البياني للدالة

لقد وجدنا جميع قيم x 0 التي يمكن اعتبارها حدود نقاط الانعطاف. بعد ذلك ، نحتاج إلى تطبيق شرط الانقلاب الكافي الأول.

التعريف 6

افترض أن لدينا دالة y = f (x) ، وهي دالة متصلة عند النقطة M (x 0 ؛ f (x 0)). علاوة على ذلك ، لها خط مماس عند هذه النقطة ، والدالة نفسها لها مشتق ثان بالقرب من هذه النقطة x 0. في هذه الحالة ، إذا كان المشتق الثاني على الجانبين الأيمن والأيسر يكتسب إشارات معاكسة ، فيمكن اعتبار هذه النقطة نقطة انعطاف.

نرى أن هذا الشرط لا يتطلب أن يكون المشتق الثاني موجودًا بالتأكيد في هذه المرحلة ؛ يكفي أن يكون بالقرب من النقطة x 0.

يتم تقديم كل ما قيل أعلاه بشكل ملائم في شكل سلسلة من الإجراءات.

  1. أولاً ، تحتاج إلى العثور على جميع abscissas x 0 من نقاط الانعطاف المحتملة ، حيث f "" (x 0) = 0 ، lim x → x 0 - 0 f "(x) = ∞ ، lim x → x 0 + 0 f" (س) = ∞.
  2. دعونا نتعرف على النقاط التي سيتغير فيها المشتق. هذه القيم هي حدود نقاط الانعطاف ، والنقاط M (x 0 ؛ f (x 0)) المقابلة لها هي نقاط الانقلاب نفسها.

من أجل الوضوح ، سنقوم بتحليل مهمتين.

مثال 3

شرط:إذا كانت الدالة y = 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x. حدد مكان وجود نقاط انعطاف وانتفاخ في الرسم البياني لهذه الوظيفة.

المحلول

يتم تحديد الوظيفة المحددة على مجموعة كاملة من الأرقام الحقيقية. نحسب المشتق الأول:

ص "= 1 10 × 4 12 - × 3 6 - 3 × 2 + 2 ×" = 1 10 4 × 3 12-3 × 2 6-6 × + 2 = = 1 10 × 3 3 - × 2 2-6 x + 2

لنجد الآن مجال المشتقة الأولى. إنها أيضًا مجموعة جميع الأعداد الحقيقية. ومن ثم ، لا يمكن تحقيق المساواة lim x → x 0 - 0 f "(x) = ∞ و lim x → x 0 + 0 f" (x) = ∞ لأي ​​قيم لـ x 0.

نحسب المشتق الثاني:

y "" = 1 10 x 3 3 - x 2 2-6 x + 2 "= 1 10 3 x 2 3-2 x 2-6 = 1 10 x 2 - x - 6

y "" = 0 ⇔ 1 10 · (x 2 - x - 6) = 0 x 2 - x - 6 = 0 D = (- 1) 2-4 · 1 · (- 6) = 25 x 1 = 1 - 25 2 = - 2 ، × 2 = 1 + 25 2 = 3

وجدنا الخطوط العريضة لنقطتي انعطاف محتملتين - 2 و 3. كل ما يتبقى لنا هو التحقق من النقطة التي سيغير فيها المشتق علامته. دعنا نرسم المحور العددي ونرسم هذه النقاط عليه ، وبعد ذلك نضع علامات المشتق الثاني على الفترات الناتجة.

توضح الأقواس اتجاه تحدب الرسم البياني في كل فترة زمنية.

ينعكس المشتق الثاني الإشارة (من موجب إلى سالب) عند النقطة مع السالب 3 ، ويمر خلالها من اليسار إلى اليمين ، ويفعل ذلك أيضًا (من سالب إلى موجب) عند النقطة التي تحتوي على الإحداثيات 3. ومن ثم ، يمكننا أن نستنتج أن x = - 2 و x = 3 هي حدود نقاط انعطاف الرسم البياني للوظيفة. سوف تتوافق مع نقاط الرسم البياني - 2 ؛ - 4 3 و 3 ؛ - 15 8.

دعونا ننظر مرة أخرى إلى صورة محور العدد والعلامات الناتجة على فترات زمنية لاستخلاص استنتاجات حول أماكن التقعر والتحدب. اتضح أن الانتفاخ سيكون موجودًا في الجزء - 2 ؛ 3 ، والتقعر على الأجزاء (- ؛ - 2] و [3 ؛ +).

يظهر حل المشكلة بوضوح على الرسم البياني: اللون الأزرق - التحدب ، الأحمر - التقعر ، اللون الأسود يعني نقاط الانعطاف.

إجابه:سيتم وضع الانتفاخ في الجزء - 2 ؛ 3 ، والتقعر على الأجزاء (- ؛ - 2] و [3 ؛ +).

مثال 4

شرط:احسب الحدود الفاصلة لكل نقاط انعطاف الرسم البياني للدالة y = 1 8 x 2 + 3 x + 2 x - 3 3 5.

المحلول

مجال دالة معينة هو مجموعة كل الأعداد الحقيقية. نحسب المشتق:

y "= 1 8 · (x 2 + 3 x + 2) x - 3 3 5" = = 1 8 · x 2 + 3 x + 2 "+ 2) x - 3 3 5" = = 1 8 2 x + 3 (x - 3) 3 5 + (x 2 + 3 x + 2) 3 5 x - 3-2 5 = 13 x 2-6 x - 39 40 (x - 3) 2 5

بخلاف الدالة ، لن يتم تعريف مشتقها الأول عندما تكون x تساوي 3 ، ولكن:

ليم س → 3 - 0 ص "(س) = 13 · (3 - 0) 2 - 6 · (3 - 0) - 39 40 · 3 - 0 - 3 2 5 = + ∞ ليم س → 3 + 0 ص" (س) = 13 (3 + 0) 2-6 (3 + 0) - 39 40 3 + 0 - 3 2 5 = +

هذا يعني أن المماس الرأسي للرسم البياني سيمر عبر هذه النقطة. لذلك ، يمكن أن تكون 3 هي حدود نقطة الانعطاف.

نحسب المشتق الثاني. نجد أيضًا مساحة تعريفه والنقاط التي يتحول عندها إلى 0:

y "= 13 x 2-6 x - 39 40 x - 3 2 5" = 1 40 13 x 2-6 x - 39 "39 x - 3 2 5" (x - 3) 4 5 = = 1 25 13 × 2-51 × + 21 (س - 3) 7 5 ، × ∈ (- ∞ ؛ 3) ∪ (3 ؛ + ∞) ص "(س) = 0 13 × 2-51 × + 21 = 0 د = (- 51) 2-4 13 21 = 1509 × 1 = 51 + 1509 26 3.456 ، × 2 = 51 - 1509 26 0.4675

لدينا نقطتا انعطاف محتملتان إضافيتان. دعنا نضعهم جميعًا على خط الأعداد ونضع علامات على الفواصل الزمنية الناتجة:

سيحدث انعكاس الإشارة عند المرور عبر كل نقطة محددة ، مما يعني أنها جميعًا نقاط انعطاف.

إجابه:دعونا نرسم الدالة ، ونضع علامات على التقعرات باللون الأحمر ، والانتفاخات باللون الأزرق ، ونقاط الانعطاف باللون الأسود:

بمعرفة أول حالة انعطاف كافية ، يمكننا تحديد النقاط المطلوبة التي لا يكون فيها وجود المشتق الثاني ضروريًا. بناءً على ذلك ، يمكن اعتبار الشرط الأول هو الأكثر عالمية ومناسبًا لحل أنواع مختلفة من المشكلات.

لاحظ أن هناك شرطين إضافيين للانعطاف ، لكن لا يمكن تطبيقهما إلا إذا كان هناك مشتق محدود عند النقطة المشار إليها.

إذا كان لدينا f "" (x 0) = 0 و f "" (x 0) ≠ 0 ، فإن x 0 سيكون حد نقطة انعطاف الرسم البياني y = f (x).

مثال 5

شرط:الدالة y = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5 معطاة. حدد ما إذا كان الرسم البياني للوظيفة سيكون له انعطاف عند النقطة 3 ؛ 4 5.

المحلول

أول شيء يجب فعله هو التأكد من أن النقطة المعينة ستنتمي على الإطلاق إلى الرسم البياني لهذه الوظيفة.

ص (3) = 1 60 3 3 - 3 20 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5

يتم تحديد الوظيفة المحددة لجميع الوسائط التي تمثل أرقامًا حقيقية. دعنا نحسب المشتقين الأول والثاني:

ص "= 1 60 × 3 - 3 20 × 2 + 7 10 × - 2 5" = 1 20 × 2 - 3 10 × + 7 10 ص "= 1 20 × 2 - 3 10 × + 7 10" = 1 10 × - 3 10 = 1 10 (× - 3)

لقد توصلنا إلى أن المشتق الثاني سيختفي إذا كان x يساوي 0. هذا يعني أنه سيتم استيفاء شرط الانعطاف الضروري لهذه النقطة. نستخدم الآن الشرط الثاني: أوجد المشتق الثالث واكتشف ما إذا كان سيتلاشى عند 3:

ص "" = 1 10 (س - 3) "= 1 10

لن يختفي المشتق الثالث لأي قيمة لـ x. لذلك ، يمكننا أن نستنتج أن هذه النقطة ستكون نقطة انعطاف الرسم البياني للوظيفة.

إجابه:لنعرض الحل في الرسم التوضيحي:

افترض أن f "(x 0) = 0، f" (x 0) = 0، ...، F (n) (x 0) = 0 و f (n + 1) (x 0) ≠ 0. In في هذه الحالة ، بالنسبة إلى n ، نحصل على أن x 0 هي حد نقطة انعطاف الرسم البياني y = f (x).

مثال 6

شرط:الدالة y = (x - 3) 5 + 1 معطاة. احسب نقاط انعطاف الرسم البياني الخاص بها.

المحلول

يتم تحديد هذه الوظيفة على مجموعة كاملة من الأرقام الحقيقية. أوجد المشتق: y "= ((x - 3) 5 + 1)" = 5 · x - 3 4. نظرًا لأنه سيتم تعريفه أيضًا لجميع القيم الصالحة للوسيطة ، سيكون المماس غير الرأسي موجودًا في أي نقطة في الرسم البياني الخاص به.

الآن دعنا نحسب القيم التي سيختفي فيها المشتق الثاني:

y "" = 5 (x - 3) 4 "= 20 x - 3 3 y" "= 0 ⇔ x - 3 = 0 x = 3

حصلنا على أنه عند x = 3 يمكن أن يحتوي الرسم البياني للدالة على نقطة انعطاف. دعنا نستخدم الشرط الثالث لتأكيد هذا:

ص "" = 20 · (س - 3) 3 "= 60 · س - 3 2 ، ص" "(3) = 60 · 3 - 3 2 = 0 ص (4) = 60 · (س - 3) 2 "= 120 (س - 3) ، ص (4) (3) = 120 (3 - 3) = 0 ص (5) = 120 (س - 3)" = 120 ، ص (5) (3) = 120 ≠ 0

لدينا n = 4 بالشرط الكافي الثالث. هذا رقم زوجي ، مما يعني أن x = 3 ستكون حدود نقطة الانقلاب وأن النقطة على الرسم البياني للوظيفة (3 ؛ 1) تتوافق معها.

إجابه:فيما يلي رسم بياني لهذه الوظيفة ، مع تحديد النتوءات والتقعرات ونقاط الانعطاف:

إذا لاحظت وجود خطأ في النص ، فيرجى تحديده والضغط على Ctrl + Enter

الرسم البياني للوظيفة ذ=و (خ)اتصل محدبفي الفترة الفاصلة (أ ؛ ب)إذا كانت تقع أسفل أي من ظلها في هذه الفترة.

الرسم البياني للوظيفة ذ=و (خ)اتصل مقعرفي الفترة الفاصلة (أ ؛ ب)إذا كانت موجودة فوق أي من ظلها في هذه الفترة.

يوضح الشكل منحنى محدب ل (أ ؛ ب)ومقعرة (ب ؛ ج).

أمثلة.

دعونا نفكر في ميزة كافية تسمح لنا بتحديد ما إذا كان الرسم البياني لوظيفة ما في فترة زمنية معينة سيكون محدبًا أم مقعرًا.

نظرية... اسمحوا ان ذ=و (خ)تفاضل من قبل (أ ؛ ب)... إذا كان في جميع نقاط الفاصل الزمني (أ ؛ ب)المشتق الثاني للدالة ذ = و (خ)سلبي ، أي F ""(x) < 0, то график функции на этом интервале выпуклый, если же F""(x)> 0 - مقعر.

دليل - إثبات... من أجل التحديد ، افترض ذلك F""(x) < 0 и докажем, что график функции будет выпуклым.

لنأخذ على الرسم البياني الوظائف ص = و (س)نقطة تعسفية م 0مع الإحداثي السيني × 0 Î ( أ; ب) وارسم من خلال النقطة م 0ظل. معادلتها. يجب أن نظهر أن التمثيل البياني للدالة على (أ ؛ ب)يقع تحت هذا الظل ، أي بنفس القيمة xمنحنى تنسيق ص = و (س)سيكون أقل من إحداثيات الظل.

إذن ، فإن معادلة المنحنى لها الشكل ص = و (س)... نشير إلى إحداثي الظل المقابل للإحداثية x... ثم . لذلك ، فإن الفرق بين إحداثيات المنحنى والماس عند نفس القيمة xسوف يكون .

فرق و (س) - و (× 0)تحويل من خلال نظرية لاجرانج ، أين جما بين xو × 0.

هكذا،

نطبق مرة أخرى نظرية لاغرانج على التعبير الموجود بين قوسين مربعين: ، أين ج 1ما بين ج 0و × 0... من خلال فرضية النظرية F ""(x) < 0. Определим знак произведения второго и третьего сомножителей.

وبالتالي ، فإن أي نقطة على المنحنى تقع أسفل مماس المنحنى لجميع القيم xو × 0 Î ( أ; ب) ، مما يعني أن المنحنى محدب. تم إثبات الجزء الثاني من النظرية بطريقة مماثلة.

أمثلة على.

تسمى النقطة الموجودة على الرسم البياني للدالة المستمرة التي تفصل الجزء المحدب من الجزء المقعر نقطة الأنحراف.

من الواضح ، عند نقطة الانعطاف ، أن الظل ، إن وجد ، يتقاطع مع المنحنى ، حيث على جانب واحد من هذه النقطة ، يقع المنحنى أسفل المماس ، ومن ناحية أخرى ، فوقه.

دعونا نحدد الشروط الكافية لنقطة معينة من المنحنى لتكون نقطة انعطاف.

نظرية... دع المنحنى يتحدد بالمعادلة ص = و (س)... لو F ""(x 0) = 0 أو F ""(x 0) غير موجود وعند المرور بالقيمة x = × 0المشتق F ""(x) علامة التغييرات ، ثم نقطة الرسم البياني للدالة مع الإحداثيات x = × 0هناك نقطة انعطاف.

دليل - إثبات... اسمحوا ان F ""(x) < 0 при x < × 0و F ""(x)> 0 من أجل x > × 0... ثم في x < × 0المنحنى محدب وعند x > × 0- مقعر. ومن هنا كانت النقطة أعلى منحنى مع حدود الإحداثية × 0هناك نقطة انعطاف. يمكن اعتبار الحالة الثانية بالمثل ، متى F ""(x)> 0 من أجل x < × 0و F ""(x) < 0 при x > × 0.

وبالتالي ، يجب البحث عن نقاط الانعطاف فقط بين تلك النقاط التي يختفي فيها المشتق الثاني أو لا يوجد.

أمثلة.ابحث عن نقاط الانعطاف وحدد فترات التحدب والتقعر للمنحنيات.


وظائف الرسومات ASYMPTOTS

عند فحص دالة ، من المهم تحديد شكل الرسم البياني الخاص بها بمسافة غير محدودة من أصل نقطة الرسم البياني.

من الأمور ذات الأهمية الخاصة الحالة عندما يقترب الرسم البياني للدالة ، عندما تتم إزالة نقطتها المتغيرة إلى ما لا نهاية ، من خط مستقيم معين بدون حدود.

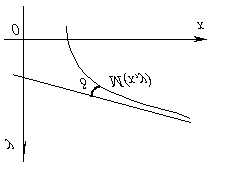
يسمى الخط المستقيم خط مقاربوظيفة الرسومات ذ = و (خ)إذا كانت المسافة من النقطة المتغيرة مرسم بياني لهذا الخط عند حذف نقطة ميميل إلى الصفر إلى اللانهاية ، أي يجب أن تقترب نقطة الرسم البياني للدالة ، لأنها تميل إلى اللانهاية ، من الخط المقارب إلى أجل غير مسمى.

يمكن للمنحنى أن يقترب من خطه المقارب ، ويبقى على جانب واحد منه أو من جوانب مختلفة ، ويعبر الخط المقارب بلا حدود عدة مرات ويمر من جانب إلى آخر.

إذا أشرنا إلى d المسافة من النقطة ممنحنى إلى الخط المقارب ، فمن الواضح أن d تميل إلى الصفر كنقطة مفي اللانهاية.

سوف نميز كذلك بين الخطوط المقاربة العمودية والمائلة.

الزوايا العمودية

دعونا في x→ × 0من أي جانب وظيفة ذ = و (خ)يزيد إلى أجل غير مسمى في القيمة المطلقة ، أي او او ... ثم يتبع من تعريف الخط المقارب أن الخط x = × 0هو خط مقارب. والعكس واضح أيضًا إذا كان الخط المستقيم x = × 0هو خط مقارب ، أي ...

وهكذا ، الخط المقارب العمودي للرسم البياني للوظيفة ص = و (س)يسمى خط مستقيم إذا و (خ)→ ∞ على الأقل في ظل أحد الشروط x→ × 0- 0 أو x → × 0 + 0, x = × 0

لذلك ، للعثور على الخطوط المقاربة العمودية للرسم البياني للدالة ذ = و (خ)بحاجة للعثور على تلك القيم x = × 0حيث تذهب الوظيفة إلى ما لا نهاية (يعاني من انقطاع لانهائي). ثم الخط المقارب العمودي لديه المعادلة x = × 0.

أمثلة.

منحنيات ASYMPTOTS

بما أن الخط المقارب هو خط مستقيم ، إذا كان المنحنى ذ = و (خ)خط مقارب مائل ، ثم ستكون معادلته ذ = ككس + ب... مهمتنا هي إيجاد المعاملات كو ب.

نظرية... على التوالي. مستقيم ذ = ككس + ببمثابة خط مقارب مائل في x→ + ∞ للرسم البياني للوظيفة ذ = و (خ)إذا وفقط إذا ... بيان مماثل صحيح أيضا ل x → –∞.

دليل - إثبات... اسمحوا ان النائب- طول المقطع يساوي المسافة من النقطة مإلى الخط المقارب. حسب الشرط. دع φ تشير إلى زاوية ميل الخط المقارب إلى المحور ثور... ثم من ΔMNPيتبع ذلك. بما أن φ زاوية ثابتة (φ ≠ π / 2) ، لكن


عند فحص دالة ورسم الرسم البياني الخاص بها في إحدى المراحل ، نحدد نقاط الانقلاب وفترات التحدب. هذه البيانات ، جنبًا إلى جنب مع فترات الزيادة والنقصان ، تجعل من الممكن تمثيل الرسم البياني للوظيفة قيد الدراسة بشكل تخطيطي.

يفترض العرض التقديمي الإضافي أنك قادر على بعض الطلبات وأنواع مختلفة.

سنبدأ دراسة المادة بالتعريفات والمفاهيم اللازمة. بعد ذلك ، سنقوم بإصدار صلة بين قيمة المشتق الثاني للدالة في فترة زمنية معينة واتجاه تحدبها. بعد ذلك ، دعنا ننتقل إلى الشروط التي تسمح لنا بتحديد نقاط انعطاف الرسم البياني للوظيفة. في جميع أنحاء النص ، سنقدم أمثلة نموذجية مع حلول مفصلة.

التنقل في الصفحة.

التحدب ، تقعر الوظيفة ، نقطة الانعطاف.

تعريف.

محدب لأسفلعلى الفاصل الزمني X ، إذا كان الرسم البياني الخاص به لا يقل عن المماس له في أي نقطة من الفترة X.

تعريف.

تسمى الوظيفة المراد تمييزها محدبعلى الفاصل الزمني X ، إذا كان الرسم البياني الخاص به ليس أعلى من المماس له في أي نقطة من الفترة X.

غالبًا ما يتم استدعاء الوظيفة المحدبة الصاعدة محدب، ومحدب لأسفل - مقعر.

ألق نظرة على الرسم الذي يوضح هذه التعريفات.

تعريف.

النقطة تسمى نقطة انعطاف الرسم البياني للوظيفة y = f (x) ، إذا كان هناك ظل عند نقطة معينة للرسم البياني للوظيفة (يمكن أن يكون موازٍ لمحور Oy) وكان هناك مجاورة للنقطة ، ضمنها الرسم البياني للوظيفة اتجاهات مختلفة من التحدب إلى يسار ويمين النقطة M.

بمعنى آخر ، تسمى النقطة M بنقطة انعطاف الرسم البياني للدالة إذا كان هناك ظل عند هذه النقطة ويغير الرسم البياني للوظيفة اتجاه التحدب الذي يمر عبره.

إذا لزم الأمر ، ارجع إلى القسم لاستدعاء شروط وجود ظل غير عمودي وعمودي.

يوضح الشكل أدناه بعض الأمثلة لنقاط انعطاف (مميزة بنقاط حمراء). لاحظ أن بعض الوظائف قد لا تحتوي على نقاط انعطاف ، في حين أن البعض الآخر قد يحتوي على نقطة انعطاف واحدة أو عدة وظائف أو عدد لا نهائي من نقاط الانقلاب.


إيجاد فترات التحدب للدالة.

دعونا نصوغ نظرية تسمح لنا بتحديد فترات التحدب لوظيفة ما.

نظرية.

إذا كانت الدالة y = f (x) لها مشتق ثانٍ محدود في الفترة X وإذا كانت المتباينة () ، فإن الرسم البياني للوظيفة به انتفاخ موجه لأسفل (لأعلى) على X.

هذه النظرية تجعل من الممكن إيجاد فترات تقعر وتحدب دالة ؛ من الضروري فقط حل المتباينات ، وعلى التوالي ، في مجال تعريف الوظيفة الأصلية.

وتجدر الإشارة إلى أن النقاط التي يتم عندها تعريف الدالة y = f (x) وعدم وجود المشتق الثاني سيتم تضمينها في فترات التقعر والتحدب.

لنلق نظرة على هذا بمثال.

مثال.

اكتشف الفترات التي يكون فيها الرسم البياني للدالة انتفاخ تصاعدي وانتفاخ نزولي.

المحلول.

مجال الوظيفة هو مجموعة الأعداد الحقيقية.

لنجد المشتق الثاني.

يتطابق مجال تعريف المشتق الثاني مع مجال تعريف الوظيفة الأصلية ، لذلك ، من أجل معرفة فترات التقعر والتحدب ، يكفي حلها ، وعلى التوالي.

لذلك ، تكون الوظيفة محدبة لأسفل على الفاصل الزمني ومحدبة لأعلى في الفترة.

الرسم التوضيحي.

يظهر جزء من الرسم البياني للوظيفة في فترة التحدب باللون الأزرق ، في فترة التقعر - باللون الأحمر.

الآن دعنا نفكر في مثال عندما لا يتطابق مجال المشتق الثاني مع مجال الدالة. في هذه الحالة ، كما أشرنا بالفعل ، يجب تضمين نقاط المجال حيث لا يوجد المشتق الثاني المحدود في فترات التحدب و (أو) التقعر.

مثال.

أوجد فترات التحدب والتقعر في الرسم البياني للدالة.

المحلول.

لنبدأ بنطاق الوظيفة:

لنجد المشتق الثاني:

مجال المشتق الثاني هو المجموعة ... كما ترى ، فإن x = 0 ينتمي إلى مجال الوظيفة الأصلية ، لكنه لا ينتمي إلى مجال المشتق الثاني. لا تنسى هذه النقطة ، سوف تحتاج إلى تضمينها في فترة التحدب و (أو) التقعر.

والآن نحل المتباينات في مجال الدالة الأصلية أيضًا. دعنا نطبق. بسط التعبير يختفي في أو ، يكون المقام عند x = 0 أو x = 1. نرسم هذه النقاط بشكل تخطيطي على خط الأعداد ونكتشف علامة التعبير في كل من الفواصل الزمنية المضمنة في مجال الوظيفة الأصلية (تظهر في المنطقة المظللة على خط الرقم السفلي). بقيمة موجبة ، نضع علامة زائد ، بقيمة سالبة - علامة ناقص.

هكذا،

و

لذلك ، بتضمين النقطة x = 0 ، نحصل على الإجابة.

في يحتوي الرسم البياني للوظيفة على تحدب موجه لأسفل ، عند - انتفاخ صاعد.

الرسم التوضيحي.

يظهر جزء من الرسم البياني للوظيفة في فترة التحدب باللون الأزرق ، على فترات التقعر - باللون الأحمر ، الخط المقارب العمودي هو الخط المنقط الأسود.

شروط الانعطاف الضرورية والكافية.

شرط انعطاف ضروري.

دعونا نصيغ شرط أساسي الانحناءوظيفة الرسومات.

دع الرسم البياني للوظيفة y = f (x) له انعطاف عند نقطة ولديه مشتق ثانٍ مستمر عند ، ثم المساواة ثابتة.

ويترتب على هذا الشرط أنه يجب البحث عن حدود نقاط الانعطاف بين تلك التي يختفي فيها المشتق الثاني للوظيفة. ولكن ، هذا الشرط ليس كافيًا ، أي ليست كل القيم التي يكون فيها المشتق الثاني مساويًا للصفر هي أبراج نقاط الانعطاف.

وتجدر الإشارة أيضًا إلى أنه وفقًا لتعريف نقطة الانعطاف ، يلزم وجود خط مماس ، كما أن الخط الرأسي ممكن أيضًا. ماذا يعني هذا؟ وهذا يعني ما يلي: يمكن أن تكون حدود نقاط الانعطاف كل شيء من مجال الوظيفة التي من أجلها و ... عادة ما تكون هذه هي النقاط التي يتلاشى عندها مقام المشتق الأول.

أول حالة انعطاف كافية.

بعد العثور على كل ما يمكن أن يكون حدود نقاط الانعطاف ، يجب عليك استخدام شرط الانحناء الكافي الأولوظيفة الرسومات.

دع الدالة y = f (x) متصلة عند نقطة ما ، ولها ظل عندها (ربما تكون رأسية) ، وهذه الوظيفة لها مشتق ثانٍ في بعض المناطق المجاورة للنقطة. بعد ذلك ، إذا كان للمشتق الثاني إشارات مختلفة داخل هذا الحي إلى اليسار وإلى اليمين ، فإن هذا هو نقطة انعطاف الرسم البياني للدالة.

كما ترى ، لا يتطلب الشرط الكافي الأول وجود المشتق الثاني عند النقطة نفسها ، ولكنه يتطلب وجودها بالقرب من النقطة.

الآن دعونا نلخص كل المعلومات في شكل خوارزمية.

خوارزمية لإيجاد نقاط انعطاف دالة.

ابحث عن كل الخطوط العريضة لنقاط الانعطاف المحتملة للرسم البياني للوظيفة (أو و ) ومعرفة ، مرورا من خلالها علامة التغييرات المشتقة الثانية. ستكون هذه القيم هي حدود نقاط الانعطاف ، وستكون النقاط المقابلة لها هي نقاط انعطاف الرسم البياني للوظيفة.

لنلقِ نظرة على مثالين لإيجاد نقاط انعطاف للتوضيح.

مثال.

أوجد نقاط الانعطاف وفترات التحدب والتقعر في الرسم البياني للوظيفة.

المحلول.

مجال الوظيفة هو مجموعة الأعداد الحقيقية بأكملها.

لنجد المشتق الأول:

مجال المشتق الأول هو أيضًا مجموعة الأعداد الحقيقية الكاملة ، وبالتالي المساواة و لا يتم تنفيذها لأي.

لنجد المشتق الثاني:

دعونا نكتشف ما هي قيم الوسيطة x يتلاشى المشتق الثاني:

وبالتالي ، فإن الخطوط العريضة لنقاط الانعطاف المحتملة هي x = -2 و x = 3.

الآن يبقى التحقق ، بمعيار الانعطاف الكافي ، عند أي من هذه النقاط يوقع تغييرات المشتق الثاني. للقيام بذلك ، ارسم النقطتين x = -2 و x = 3 على المحور العددي وكما في طريقة الفاصل المعمم، ضع علامات المشتق الثاني على كل فترة. تحت كل فترة زمنية ، يتم عرض اتجاه تحدب الرسم البياني للوظيفة بشكل تخطيطي بواسطة الأقواس.

المشتق الثاني يغير إشارة من موجب إلى سالب ، ويمر بالنقطة x = -2 من اليسار إلى اليمين ، ويغير إشارة من سالب إلى زائد ، ويمر عبر x = 3. لذلك ، فإن كل من x = -2 و x = 3 هما حدود نقاط انعطاف الرسم البياني للوظيفة. تتوافق مع نقاط الرسم البياني و.

بالنظر مرة أخرى إلى محور العدد وعلامات المشتق الثاني على فتراته ، يمكن للمرء أن يستنتج استنتاجًا حول فترات التحدب والتقعر. الرسم البياني للدالة محدب على الفاصل ومقعّر على الفواصل الزمنية و.

الرسم التوضيحي.

يظهر جزء من الرسم البياني للوظيفة في فترة التحدب باللون الأزرق ، على فترات التقعر - باللون الأحمر ، تظهر نقاط الانعطاف بنقاط سوداء.

مثال.

أوجد الخطوط العريضة لجميع نقاط انعطاف الرسم البياني للوظيفة .

المحلول.

مجال هذه الوظيفة هو مجموعة الأعداد الحقيقية بأكملها.

لنجد المشتق.

المشتق الأول ، على عكس الوظيفة الأصلية ، غير معرّف لـ x = 3. ولكن و ... لذلك ، عند نقطة لها حدود المحور x = 3 ، يوجد مماس رأسي لمنحنى الدالة الأصلية. وبالتالي ، يمكن أن تكون x = 3 هي حد نقطة انعطاف الرسم البياني للوظيفة.

نجد المشتق الثاني ومجال تعريفه والنقاط التي يتلاشى عندها:

تم الحصول على اثنين من الاحتمالات الأخرى المحتملة لنقاط الانعطاف. نحدد جميع النقاط الثلاث على خط الأعداد ونحدد علامة المشتق الثاني في كل من الفواصل الزمنية التي تم الحصول عليها.

علامة التغييرات المشتقة الثانية ، التي تمر عبر كل نقطة ، لذلك ، جميعها عبارة عن حدود لنقاط الانعطاف.

الرسم التوضيحي.

تظهر أجزاء من الرسم البياني للوظائف على فترات التحدب باللون الأزرق ، على فترات التقعر - باللون الأحمر ، تظهر نقاط الانعطاف بنقاط سوداء.

يسمح الشرط الأول الكافي لانقلاب الرسم البياني للوظيفة بتحديد نقاط الانعطاف ولا يتطلب وجود المشتق الثاني فيها. لذلك ، يمكن اعتبار الشرط الأول الكافي عالميًا والأكثر استخدامًا.

سنقوم الآن بصياغة شرطين إضافيين كافيين للانقلاب ، لكنهما لا ينطبقان إلا إذا كان هناك مشتق محدود عند نقطة الانقلاب إلى ترتيب معين.

حالة انعطاف كافية ثانية.

إذا كان ، a ، فإن حدود نقطة انعطاف الرسم البياني للدالة y = f (x) x = 3 غير صفرية.

من الواضح أن قيمة المشتق الثالث ليست صفرية لأي x ، بما في ذلك x = 3. لذلك ، وفقًا للشرط الثاني الكافي لانقلاب الرسم البياني للوظيفة ، فإن النقطة هي نقطة الانعطاف.

الرسم التوضيحي.

ثالث شرط انعطاف كاف.

لنفترض ، a ، إذن إذا كان n عددًا زوجيًا ، فهو إذن نقطة الانعطاف في الرسم البياني للدالة y = f (x).

مثال.

أوجد نقاط انعطاف الرسم البياني للوظيفة .

المحلول.

يتم تحديد الوظيفة على مجموعة الأرقام الحقيقية بأكملها.

لنجد مشتقها: ... من الواضح أنه يتم تعريفه أيضًا لجميع x الحقيقي ، لذلك يوجد في أي نقطة من الرسم البياني خط مماس غير عمودي.

لنحدد قيم x التي يختفي عندها المشتق الثاني.

وهكذا ، عند النقطة التي تكون فيها الإحداثيات س = 3 ، قد يكون هناك انعطاف في الرسم البياني للوظيفة. للتأكد من أن x = 3 هي بالفعل حدود نقطة الانعطاف ، نستخدم الشرط الكافي الثالث.

وفقًا للشرط الثالث الكافي لانعكاس الرسم البياني للوظيفة ، لدينا n = 4 (المشتق الخامس يختفي) - حتى ، وبالتالي فإن x = 3 هي حدود نقطة الانعطاف وتتوافق مع النقطة الموجودة على الرسم البياني من الوظيفة (3 ؛ 1).

الرسم التوضيحي.

يظهر جزء من الرسم البياني للوظيفة في فترة التحدب باللون الأزرق ، في فترة التقعر - باللون الأحمر ، تظهر نقطة الانعطاف بنقطة سوداء.

يبقى للنظر التواءات التحدب والتقعر والمنحنى... لنبدأ بالتمرين الذي يحبه الزوار كثيرًا. يرجى الوقوف والانحناء للأمام أو للخلف. هذا انتفاخ. الآن مد ذراعيك أمامك ، راح يديك لأعلى وتخيل أنك تمسك بسجل كبير على صدرك ... ... حسنًا ، إذا كنت لا تحب السجل ، فليكن شيئًا آخر / شخصًا =) هذا تقعر . يحتوي عدد من المصادر على مصطلحات مترادفة انتفاخو انتفاخلكني من دعاة الأسماء القصيرة.

! انتباه : بعض المؤلفين حدد التحدب والتقعر على العكس تمامًا... هذا أيضًا صحيح رياضيًا ومنطقيًا ، لكنه غالبًا ما يكون غير صحيح تمامًا من وجهة نظر موضوعية ، بما في ذلك على مستوى فهمنا الصغير للمصطلحات. لذلك ، على سبيل المثال ، تسمى العدسة ثنائية الوجه بالعدسة ذات "الدرنات" ، ولكن ليس مع "المنخفضات" (التجويف الثنائي).
وعلى سبيل المثال ، سرير "مقعر" - لا يزال من الواضح أنه لا "يلتصق" =) (ومع ذلك ، إذا قمت بالزحف تحته ، فسوف نتحدث عن الانتفاخ ؛ =)) ألتزم بنهج يتوافق مع الطبيعي الجمعيات البشرية.

يعد التعريف الرسمي للتحدب والتقعر في الرسم البياني صعبًا نوعًا ما بالنسبة لإبريق الشاي ، لذلك نقصر أنفسنا على التفسير الهندسي للمفهوم باستخدام أمثلة محددة. النظر في الرسم البياني للدالة التي مستمرعلى خط الأعداد الصحيح:

من السهل البناء به التحولات الهندسيةوربما يعرف الكثير من القراء كيفية اشتقاقها من القطع المكافئ المكعب.

لنتصل وترربط الجزء نقطتان مختلفتانالفنون التصويرية.

الرسم البياني للدالة هو محدبفي بعض الفواصل الزمنية ، إذا كان موجودًا ليس أقلأي وتر من الفترة المحددة. خط الاختبار محدب ، ومن الواضح أنه يوجد هنا أي جزء من الرسم البياني أعلاه وتر... لتوضيح التعريف ، قمت برسم ثلاثة خطوط سوداء.

وظائف الرسم البياني هي مقعرفي الفاصل الزمني ، إذا كان موجودًا ليس أعلىأي وتر من هذه الفترة. في هذا المثال ، يكون المريض مقعرًا بينهما. يوضح زوج من المقاطع البنية بشكل مقنع أن أي جزء من المخطط يقع تحته وتر.

النقطة التي يتغير عندها الرسم البياني من التحدب إلى التقعر أويسمى التقعر إلى التحدب نقطة الأنحراف... لدينا في نسخة واحدة (الحالة الأولى) ، وعمليًا ، يمكن أن تعني نقطة الانعطاف كلاً من النقطة الخضراء التي تنتمي إلى الخط نفسه وقيمة "x".

مهم!يجب رسم الفواصل الزائدة في الرسم البياني بعناية و بسلاسة شديدة... كل أنواع "المخالفات" و "الخشونة" غير مقبولة. إنه مجرد تمرين بسيط.

يتم إعطاء النهج الثاني لتعريف التحدب / التقعر من الناحية النظرية من حيث الظل:

محدبيقع الرسم البياني على الفاصل الزمني ليس أعلىالمماس المرسوم إليها عند نقطة اعتباطية من هذه الفترة الفاصلة. مقعرلكن في الفاصل الزمني الرسم البياني - ليس أقلأي ظل في هذه الفترة.

القطع الزائد مقعر في الفترة الزمنية ومحدب على:

عند المرور عبر الأصل ، يتغير التقعر إلى التحدب ، ولكن النقطة لا تعدنقطة انعطاف ، منذ الوظيفة لم يحددفيه.

يمكن العثور على بيانات ونظريات أكثر صرامة حول هذا الموضوع في الكتاب المدرسي ، وننتقل إلى الجزء العملي الغني:

كيفية إيجاد فترات محدبة ، فترات التقعر
ونقاط انعطاف الرسم البياني؟

المادة بسيطة ، استنسل وتتكرر هيكليًا دراسة الوظيفة القصوى.

يميز التحدب / التقعر في الرسم البيانيالمشتق الثاني وظيفة.

دع الدالة تكون قابلة للاشتقاق مرتين في فترة ما. ثم:

- إذا كان المشتق الثاني في فترة زمنية ، فإن الرسم البياني للوظيفة محدب في هذه الفترة ؛

- إذا كان المشتق الثاني في فترة زمنية ، فإن الرسم البياني للدالة مقعر في هذه الفترة.

على حساب علامات المشتق الثاني في المساحات المفتوحة للمؤسسات التعليمية ، تمشي جمعية ما قبل التاريخ: "-" تُظهر أنه "لا يمكن سكب الماء في الرسم البياني للوظيفة" (الانتفاخ) ،
و "+" - "يعطي مثل هذه الفرصة" (التقعر).

متطلبات الانحناء

إذا كان هناك انعطاف في الرسم البياني للوظيفة عند هذه النقطة، من ثم:
أو القيمة غير موجودة(دعونا نفكك ، اقرأ!).

هذه العبارة تعني أن الوظيفة مستمرعند نقطة ما ، وفي هذه الحالة ، يمكن تمييزها مرتين في بعض المناطق المجاورة لها.

تشير ضرورة الشرط إلى أن العكس ليس صحيحًا دائمًا. أي من المساواة (أو عدم وجود قيمة) ليس بعدوجود انعطاف للرسم البياني للوظيفة عند نقطة ما. لكن في كلتا الحالتين يسمونه النقطة الحرجة للمشتق الثاني.

حالة شبك كافية

إذا تغير المشتق الثاني عند المرور عبر نقطة ، فعند هذه النقطة يكون هناك انعطاف في الرسم البياني للوظيفة.

قد لا توجد نقاط انعطاف (تم استيفاء أحد الأمثلة بالفعل) على الإطلاق ، وبهذا المعنى ، فإن بعض العينات الأولية تكون إرشادية. دعنا نحلل المشتق الثاني للدالة:

يتم الحصول على دالة ثابتة موجبة ، أي ، لأي قيمة "x"... حقائق السطح: القطع المكافئ مقعر طوال الوقت مجالات التعريف، لا توجد نقاط انعطاف. من السهل أن نرى أن المعامل السالب عند "يعكس" القطع المكافئ ويجعله محدبًا (والذي سيتم الإبلاغ عنه بواسطة المشتق الثاني - دالة ثابتة سالبة).

الدالة الأسية مقعرة أيضًا لـ:

لأي قيمة "س".

بالطبع ، لا يحتوي الرسم البياني على نقاط انعطاف.

دعونا نفحص من أجل التحدب / التقعر الرسم البياني للوظيفة اللوغاريتمية:

وبالتالي ، فإن فرع اللوغاريتم محدب في الفترة. يتم تعريف المشتق الثاني أيضًا على الفترة الزمنية ، لكن ضع في الاعتبار ذلك ممنوعنظرًا لأن هذا الفاصل الزمني غير مدرج في نطاقالمهام. الشرط واضح - طالما لا يوجد رسم بياني للوغاريتم ، إذن ، بالطبع ، لا يوجد أي ذكر لأي تحدب / تقعر / انعكاس للكلام.

كما ترون ، كل شيء يشبه القصة عن كثب الزيادة والنقصان والحد الأقصى للوظيفة... يبدو مثلي خوارزمية دراسة الرسم البياني وظيفةللتحدب والتقعر ووجود مكامن الخلل:

2) البحث عن القيم الحرجة. للقيام بذلك ، نأخذ المشتق الثاني ونحل المعادلة. تعتبر النقاط التي لا يوجد عندها المشتق الثاني ، ولكنها مدرجة في مجال الوظيفة نفسها ، حرجة أيضًا!

3) نحدد على خط الأعداد جميع نقاط الانقطاع الموجودة والنقاط الحرجة ( قد لا يظهر أحد أو الآخر - فأنت لست بحاجة إلى رسم أي شيء (كما في حالة بسيطة جدًا) ، يكفي أن تقصر نفسك على تعليق مكتوب). من خلال طريقة الفتراتنحدد العلامات على الفترات التي تم الحصول عليها. كما أوضح للتو ، ينبغي للمرء أن ينظر فقط اولئكالفجوات التي تقع ضمن نطاق الوظيفة. نستخلص استنتاجات حول نقاط التحدب / التقعر والانعطاف للرسم البياني للوظيفة. نعطي الجواب.

حاول تطبيق الخوارزمية لفظيًا على الوظائف ... في الحالة الثانية ، بالمناسبة ، هناك مثال عندما لا يكون هناك انعطاف في الرسم البياني عند النقطة الحرجة. ومع ذلك ، لنبدأ بمهام أكثر صعوبة قليلاً:

مثال 1


المحلول:
1) يتم تعريف الوظيفة ومستمرة على خط الأعداد الصحيح. ممتاز.

2) أوجد المشتق الثاني. من الممكن إجراء مكعبات مسبقًا ، لكنها أكثر ربحية للاستخدام قاعدة تمايز الوظائف المعقدة:

لاحظ أن ، مما يعني أن الوظيفة غير متناقص... على الرغم من أن هذا لا ينطبق على المهمة ، فمن المستحسن دائمًا الانتباه إلى هذه الحقائق.

لنجد النقاط الحرجة للمشتق الثاني:

- نقطة حرجة

3) دعونا نتحقق من استيفاء شرط الانعطاف الكافي. دعونا نحدد علامات المشتق الثاني على الفترات التي تم الحصول عليها.

انتباه!نحن الآن نعمل مع المشتق الثاني (وليس مع الدالة!)

نتيجة لذلك ، يتم الحصول على نقطة حرجة واحدة:.

3) نحدد نقطتين من عدم الاستمرارية على خط الأعداد ، وهي نقطة حرجة ونحدد علامات المشتق الثاني على الفترات الزمنية التي تم الحصول عليها:

أذكرك خدعة مهمة طريقة الفاصل، مما يسمح لك بتسريع الحل بشكل كبير. المشتق الثاني اتضح أنه مرهق للغاية ، لذلك ليس من الضروري حساب قيمه ، يكفي عمل "تقدير" في كل فترة. دعنا نختار ، على سبيل المثال ، نقطة تنتمي إلى الفترة اليسرى ،
وإجراء الاستبدال:

الآن دعنا نحلل العوامل:

وبالتالي ، فإن "سالب" و "زائد" يعطيان علامة "موجب" ، مما يعني أن المشتق الثاني موجب خلال الفترة بأكملها.

الإجراءات التي تم التعليق عليها سهلة التنفيذ لفظيًا. بالإضافة إلى ذلك ، من المفيد تجاهل العامل تمامًا - فهو إيجابي لأي "س" ولا يؤثر على علامات المشتق الثاني.

إذن ما هي المعلومات التي زودتنا بها؟

إجابه: الرسم البياني للدالة مقعر عند ومحدب على ... بالأصل (انه واضح )هناك انعطاف في الجدول.

عند المرور عبر النقاط ، يغير المشتق الثاني أيضًا الإشارة ، لكنها لا تعتبر نقاط انعطاف ، لأن الوظيفة تعاني فيها فترات راحة لا نهاية لها.

في المثال المفكك ، المشتق الأول يخبرنا عن نمو الوظيفة طوال الوقت مجالات التعريف... سيكون هناك دائمًا مثل هذه الهدية الترويجية =) بالإضافة إلى ذلك ، من الواضح أن هناك ثلاثة الخطوط المقاربة... تم الحصول على الكثير من البيانات ، مما يسمح لنا بتمثيل مظهر الرسم البياني بدرجة عالية من الموثوقية. بالنسبة إلى الكومة ، تكون الوظيفة غريبة أيضًا. بناءً على الحقائق الثابتة ، حاول الرسم على مسودة. الصورة في نهاية الدرس.

التنازل عن حل مستقل:

مثال 6

افحص الرسم البياني للدالة من أجل التحدب والتقعر واعثر على نقاط انعطاف الرسم البياني ، إذا كانت موجودة.

لا يوجد رسم في العينة ، لكن لا يُمنع طرح فرضية ؛)

نطحن المادة دون ترقيم نقاط الخوارزمية:

مثال 7

افحص الرسم البياني للدالة من أجل التحدب والتقعر واعثر على نقاط الانعطاف ، إن وجدت.

المحلول: الوظيفة تدوم استراحة لا نهاية لهافي هذه النقطة.

كالعادة كل شيء على ما يرام معنا:

المشتقات ليست هي الأصعب ، الشيء الرئيسي هو توخي الحذر مع "شعرهم".
تم العثور على نقطتين حرجتين من المشتق الثاني في المارفيت المستحث:

دعونا نحدد العلامات على الفترات الزمنية التي تم الحصول عليها:

يوجد انعطاف في الرسم البياني عند النقطة ، نجد إحداثي النقطة:

عند المرور بنقطة ، فإن المشتق الثاني لا يغير العلامة ، وبالتالي ، لا يوجد انعطاف في الرسم البياني.

إجابه: فترات محدبة: ؛ فاصل التقعر :؛ نقطة الأنحراف:.

دعنا نلقي نظرة على بعض الأمثلة النهائية مع أجراس وصفارات إضافية:

المثال 8

أوجد فترات التحدب والتقعر ونقاط انعطاف الرسم البياني

المحلول: مع إيجاد مجالات التعريفلا توجد مشاكل خاصة:
، في حين أن الوظيفة بها انقطاعات عند النقاط.

نسير في الطريق المطروق:

- نقطة حرجة.

دعونا نحدد العلامات ، مع مراعاة الفواصل الزمنية فقط من نطاق الوظيفة:

يوجد انعطاف في الرسم البياني عند النقطة ، احسب الإحداثي: