Znajdź wszystkie asymptoty wykresu funkcji. Asymptoty wykresu funkcji. Asymptoty pionowe wykresu funkcji
Asymptoty wykresu funkcji
Duch asymptoty od dawna błąka się po serwisie, by wreszcie zmaterializować się w osobnym artykule i zachwycić zdziwionych czytelników pełna eksploracja funkcji... Znalezienie asymptot wykresu jest jedną z niewielu części określonego zadania, które jest omówione w kursie szkolnym tylko w porządku ogólnym, ponieważ zdarzenia obracają się wokół obliczeń granice funkcji, ale nadal należą do wyższej matematyki. Goście, którzy są słabo zaznajomieni z analizą matematyczną, podpowiedź, jak sądzę, jest jasna ;-) ... stop-stop, dokąd idziesz? Limity- To jest łatwe!
Przykłady asymptot napotkaliśmy od razu w pierwszej lekcji na temat wykresy funkcji elementarnych, a teraz temat jest szczegółowo rozważany.
Czym więc jest asymptota?
Wyobrażać sobie punkt zmienny, który „jeździ” zgodnie z harmonogramem funkcji. Asymptota to proste, do czego nieograniczenie blisko wykres funkcji zbliża się, gdy przesuwa się jej punkt zmiennej do nieskończoności.
Notatka : definicja ma sens, jeśli potrzebujesz sformułowania w notacji analizy matematycznej, zapoznaj się z podręcznikiem.
Na płaszczyźnie asymptoty są klasyfikowane zgodnie z ich naturalnym położeniem:
1) Asymptoty pionowe, które są podane przez równanie postaci, gdzie „alfa” jest liczbą rzeczywistą. Popularny przedstawiciel definiuje samą oś y,
z napadem łagodnych nudności przypominamy sobie hiperbolę.
2) Asymptoty ukośne tradycyjnie nagrywane równanie linii prostej ze spadkiem. Czasami szczególny przypadek jest wyróżniany jako osobna grupa - asymptoty poziome... Na przykład ta sama hiperbola z asymptotą.
Ruszamy żwawo, przejdźmy do tematu krótką serią broni automatycznej:
Ile asymptot może mieć wykres funkcji?
Brak, jeden, dwa, trzy... albo nieskończenie wiele. Nie zajdziemy daleko po przykłady, pamiętaj podstawowe funkcje... Parabola, parabola sześcienna, sinusoida w ogóle nie mają asymptot. Wykres wykładniczej funkcji logarytmicznej ma pojedynczą asymptotę. Arctangens i arccotangens mają dwa, a tangens i cotangens są nieskończenie liczne. Nierzadko zdarza się, że wykres zawiera zarówno asymptoty poziome, jak i pionowe. Hiperbola, zawsze będzie cię kochać.
Co znaczy ?
Asymptoty pionowe wykresu funkcji
Zwykle znajduje się pionowa asymptota grafu w punkcie nieskończonego załamania Funkcje. To proste: jeśli funkcja cierpi na nieskończoną nieciągłość w punkcie, to linia prosta podana przez równanie jest pionową asymptotą wykresu.
Notatka : Zauważ, że notacja jest używana w odniesieniu do dwóch zupełnie różnych pojęć. Punkt jest implikowany lub równanie prostej - w zależności od kontekstu.
Tak więc, aby ustalić obecność asymptoty pionowej w punkcie, wystarczy wykazać, że przynajmniej jeden z jednostronnych granic 
nieskończony. Najczęściej jest to punkt, w którym mianownik funkcji wynosi zero. W związku z tym w ostatnich przykładach lekcji znaleźliśmy już pionowe asymptoty. o ciągłości funkcji... Ale w niektórych przypadkach istnieje tylko jedna jednostronna granica, a jeśli jest nieskończona, to znowu - kochaj i faworyzuj pionową asymptotę. Najprostsza ilustracja: i oś rzędnych (patrz. Wykresy i własności funkcji elementarnych).
Z powyższego wynika również oczywisty fakt: jeśli funkcja jest włączona w sposób ciągły, to nie ma pionowych asymptot... Z jakiegoś powodu przyszła mi do głowy parabola. Rzeczywiście, gdzie można tu „przykleić” linię prostą? ... tak ... rozumiem ... Zwolennicy wujka Freuda byli histeryczni =)
Stwierdzenie odwrotne generalnie nie jest prawdziwe: na przykład funkcja nie jest zdefiniowana na całej osi liczbowej, ale jest całkowicie pozbawiona asymptot.
Asymptoty nachylone wykresu funkcji
Ukośne (jako przypadek szczególny - poziomy) asymptoty można narysować, jeśli argument funkcji ma tendencję do „plus nieskończoność” lub „minus nieskończoność”. W związku z tym wykres funkcji nie może mieć więcej niż dwie asymptoty ukośne... Na przykład wykres funkcji wykładniczej ma pojedynczą poziomą asymptotę w, a wykres arcus tangensa ma dwie takie asymptoty i różne.
Kiedy wykres tu i ówdzie zbliża się do jedynej ukośnej asymptoty, zwyczajowo łączy się „nieskończoność” w jednym zapisie. Na przykład ... dobrze zgadłeś :.
Ogólna zasada praktyczna:
Jeśli są dwa finał limit 
, to linia prosta jest ukośną asymptotą wykresu funkcji przy. Jeśli przynajmniej jeden z wymienionych granic jest nieskończona, to asymptota ukośna jest nieobecna.
Notatka : formuły zachowują ważność, jeśli „x” dąży tylko do „plus nieskończoność” lub tylko do „minus nieskończoności”.
Pokażmy, że parabola nie ma asymptot ukośnych: 
Granica jest nieskończona, co oznacza, że nie ma asymptoty ukośnej. Zauważ, że w znalezieniu limitu 
potrzeba nie była już potrzebna, ponieważ odpowiedź została już otrzymana.
Notatka
: jeśli masz (lub będziesz miał) trudności ze zrozumieniem znaków „plus-minus”, „minus-plus”, zapoznaj się z pomocą na początku lekcji
na nieskończenie małych funkcjach, gdzie powiedziałem, jak poprawnie zinterpretować te znaki.
Oczywiście żadna funkcja kwadratowa, sześcienna, wielomian stopnia czwartego i wyższego również nie ma asymptot ukośnych.
Teraz upewnijmy się, że wykres nie ma również ukośnej asymptoty. Aby ujawnić niepewność, używamy Zasada L'Hôpital:
, który wymagał weryfikacji.
Bo funkcja rośnie w nieskończoność, ale nie ma prostej, do której zbliżałby się jej wykres nieskończenie blisko.
Przejdźmy do praktycznej części lekcji:
Jak znaleźć asymptoty wykresu funkcji?
Tak sformułowane jest typowe zadanie, które polega na znalezieniu WSZYSTKICH asymptot wykresu (pionowej, ukośnej / poziomej). Chociaż, żeby być bardziej precyzyjnym w sformułowaniu pytania, mówimy o badaniu na obecność asymptot (w końcu może ich wcale nie być). Zacznijmy od czegoś prostego:
Przykład 1
Znajdź asymptoty wykresu funkcji
Rozwiązanie wygodnie jest podzielić go na dwa punkty:
1) Najpierw sprawdzamy, czy istnieją pionowe asymptoty. Mianownik znika w momencie i od razu widać, że w danym momencie funkcja cierpi niekończąca się przerwa, a linia prosta podana przez równanie jest pionową asymptotą wykresu funkcji. Ale przed sformułowaniem takiego wniosku konieczne jest znalezienie jednostronnych granic: 
Przypominam technikę obliczeń, o której podobnie rozwodziłem się w artykule Ciągłość funkcji. Punkty przerwania... Podstawiamy w wyrażeniu pod znakiem limitu zamiast „x”. Nic ciekawego w liczniku:
.
Ale w mianowniku okazuje się nieskończenie mała liczba ujemna:
, decyduje również o losie limitu.
Granica lewostronna jest nieskończona i w zasadzie możliwe jest już wydanie werdyktu o obecności asymptoty pionowej. Ale jednostronne ograniczenia są potrzebne nie tylko do tego - POMAGAJĄ ZROZUMIEĆ, JAK znajduje się wykres funkcji i go wykreśla PRAWIDŁOWO... Dlatego musimy również obliczyć prawą granicę: 
Wniosek: granice jednostronne są nieskończone, co oznacza, że linia prosta jest pionową asymptotą wykresu funkcji przy.
Pierwszy limit skończone, co oznacza, że należy „kontynuować rozmowę” i znaleźć drugi limit:
Drugi limit też skończone.
Tak więc nasza asymptota to:
Wniosek: linia prosta podana przez równanie jest poziomą asymptotą wykresu funkcji przy.
Aby znaleźć poziomą asymptotę
możesz użyć uproszczonej formuły:
Jeśli jest skończone granica, to linia prosta jest poziomą asymptotą wykresu funkcji przy.
Łatwo zauważyć, że licznik i mianownik funkcji ta sama kolejność wzrostu, co oznacza, że pożądana granica będzie skończona: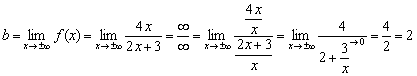 
Odpowiadać:
Pod warunkiem, że nie musisz kończyć rysunku, ale jeśli w pełnym rozkwicie badanie funkcji, a następnie na szkicu od razu szkicujemy: 
W oparciu o trzy znalezione limity, spróbuj samodzielnie ustalić, jak może znajdować się wykres funkcji. Czy to naprawdę trudne? Znajdź 5-6-7-8 punktów i zaznacz je na rysunku. Jednak wykres tej funkcji jest zbudowany przy użyciu przekształcenia wykresu funkcji elementarnej, a czytelnicy, którzy dokładnie przeanalizowali przykład 21 tego artykułu, z łatwością odgadną, czym jest ta krzywa.
Przykład 2
Znajdź asymptoty wykresu funkcji
To jest przykład rozwiązania „zrób to sam”. Przypomnę, że proces można wygodnie podzielić na dwa punkty - asymptoty pionowe i asymptoty ukośne. W przykładowym rozwiązaniu pozioma asymptota znajduje się za pomocą uproszczonego schematu.
W praktyce najczęściej spotyka się funkcje ułamkowo-racjonalne, a po treningu na hiperbolach skomplikujemy zadanie:
Przykład 3
Znajdź asymptoty wykresu funkcji 
Rozwiązanie: Raz, dwa i gotowe:
1) Znaleziono pionowe asymptoty w punktach nieskończonej nieciągłości, więc musisz sprawdzić, czy mianownik zniknął. Rozwiążemy! równanie kwadratowe:
Wyróżnik jest dodatni, więc równanie ma dwa pierwiastki rzeczywiste, a praca jest znacznie dodana =) 
W celu dalszego znalezienia granic jednostronnych wygodnie jest rozłożyć na czynniki kwadrat trójmian:
(w przypadku notacji zwartej w pierwszym nawiasie umieszczono „minus”). Aby być po bezpiecznej stronie, dokonamy kontroli, mentalnie lub w przeciągu, otwierając wsporniki.
Przepisujemy funkcję jako 
Znajdźmy jednostronne granice w punkcie: 
A w punkcie: 
Zatem linie proste są pionowymi asymptotami wykresu rozważanej funkcji.
2) Patrząc na funkcję 
, to jest całkiem oczywiste, że granica będzie skończona i mamy asymptotę poziomą. Pokażmy w skrócie jego obecność: 
Zatem linia prosta (oś odciętych) jest poziomą asymptotą wykresu tej funkcji.
Odpowiadać:
Znalezione granice i asymptoty dostarczają wielu informacji o wykresie funkcji. Spróbuj zwizualizować rysunek, biorąc pod uwagę następujące fakty: 
Naszkicuj swoją wersję wykresu na szkicu.
Oczywiście znalezione granice nie określają jednoznacznie rodzaju wykresu i można się pomylić, ale samo ćwiczenie będzie nieocenioną pomocą podczas pełne badanie funkcji... Prawidłowy obrazek znajduje się na końcu lekcji.
Przykład 4
Znajdź asymptoty wykresu funkcji
Przykład 5
Znajdź asymptoty wykresu funkcji 
To są zadania do samodzielnego rozwiązania. Oba wykresy ponownie mają asymptoty poziome, które są natychmiast wykrywane przez następujące cechy: w przykładzie 4 kolejność wzrostu mianownik jeszcze niż kolejność wzrostu licznika, a w przykładzie 5 licznik i mianownik ta sama kolejność wzrostu... W roztworze próbki pierwsza funkcja jest badana pod kątem obecności ukośnych asymptot w sposób kompletny, a druga - przez granicę.
Asymptoty poziome, w moim subiektywnym odczuciu, są zauważalnie częstsze niż te, które są „prawdziwie przechylone”. Długo oczekiwany przypadek ogólny:
Przykład 6
Znajdź asymptoty wykresu funkcji 
Rozwiązanie: klasyka gatunku:
1) Ponieważ mianownik jest dodatni, funkcja ciągły na całej osi liczbowej i nie ma pionowych asymptot. …Czy to jest dobre? Niewłaściwe słowo - świetnie! Punkt 1 jest zamknięty.
2) Sprawdź obecność ukośnych asymptot:
Pierwszy limit skończone, więc idziemy dalej. Przy obliczaniu drugiego limitu do wyeliminowania niepewności "nieskończoność minus nieskończoność" sprowadzamy wyrażenie do wspólnego mianownika: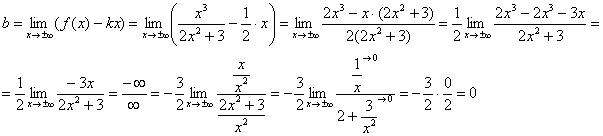 
Drugi limit też skończone, dlatego wykres rozważanej funkcji ma asymptotę ukośną:
Wniosek:
Tak więc, gdy wykres funkcji 
nieskończenie blisko zbliża się do linii prostej: 
Zauważ, że przecina ona swoją ukośną asymptotę w punkcie początkowym, a takie punkty przecięcia są całkiem do przyjęcia - ważne jest, aby "wszystko było normalne" w nieskończoności (w rzeczywistości mowa o asymptotach jest właśnie tam).
Przykład 7
Znajdź asymptoty wykresu funkcji
Rozwiązanie: Nie ma nic specjalnego do komentowania, więc sporządzę przybliżoną próbkę czystego rozwiązania:
1) Asymptoty pionowe. Zbadaj punkt.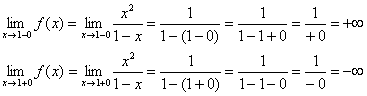 
Linia prosta jest pionową asymptotą wykresu w punkcie.
2) Asymptoty ukośne: 
Linia prosta jest ukośną asymptotą dla wykresu o godz.
Odpowiadać: 
Znalezione jednostronne granice i asymptoty z dużą pewnością pozwalają nam zasugerować, jak wygląda wykres tej funkcji. Prawidłowy rysunek na końcu lekcji.
Przykład 8
Znajdź asymptoty wykresu funkcji
Jest to przykład niezależnego rozwiązania, dla wygody obliczania niektórych limitów można podzielić licznik przez mianownik terminu przez termin. I znowu, analizując uzyskane wyniki, spróbuj narysować wykres tej funkcji.
Oczywiście właścicielami „prawdziwych” asymptot ukośnych są wykresy tych funkcji ułamkowo-wymiernych, dla których najwyższy stopień licznika jeszcze jeden najwyższy stopień mianownika. Jeśli jest większa, ukośna asymptota już nie będzie istnieć (na przykład).
Ale w życiu zdarzają się inne cuda:
Przykład 9
Przykład 11
Zbadaj wykres funkcji pod kątem obecności asymptot
Rozwiązanie: to oczywiste, że 
, dlatego rozważamy tylko prawą półpłaszczyznę, na której znajduje się wykres funkcji.
Zatem linia prosta (oś rzędnych) jest pionową asymptotą wykresu funkcji w.
2) Badanie asymptoty ukośnej można przeprowadzić zgodnie z pełnym schematem, ale w artykule Zasady L'Hôpital odkryliśmy, że funkcja liniowa wyższego rzędu wzrostu niż logarytmiczna, a więc: 
(patrz przykład 1 tej samej lekcji).
Wniosek: oś odciętych jest poziomą asymptotą wykresu funkcji przy.
Odpowiadać:
, Jeśli ;
, Jeśli .
Rysowanie dla jasności: 
Interesujące jest to, że pozornie podobna funkcja nie ma w ogóle asymptotek (chętni mogą to sprawdzić).
Dwa końcowe przykłady do samodzielnej nauki:
Przykład 12
Zbadaj wykres funkcji pod kątem obecności asymptot 
- (z greki. neg. częste i symptotos zbiegające się). Linia prosta ciągle zbliża się do krzywej i spotyka ją dopiero w nieskończoności. Słownik wyrazów obcych zawartych w języku rosyjskim. Chudinov AN, 1910. ASYMPTOT z ... ... Słownik obcych słów języka rosyjskiego
ASYMPTOTA- (z greckiego asymptotos nie pokrywające się), linia prosta, do której nieskończona gałąź krzywej zbliża się w nieskończoność, na przykład asymptota hiperboli ... Współczesna encyklopedia
ASYMPTOTA- (z greckiego asymptotos nie pokrywające się) krzywej o nieskończonej gałęzi, prostej, do której ta gałąź zbliża się bez ograniczeń, na przykład asymptota hiperboli ... Wielki słownik encyklopedyczny
asymptota- Linia prosta, do której krzywa stopniowo się zbliża. asymptota Linia prosta, do której zmierza krzywa pewnej funkcji (nigdy jej nie osiąga) o nieskończonej gałęzi, gdy jej argument rośnie bez ograniczeń lub ... Poradnik tłumacza technicznego
Asymptota- (z greckiego asymptotos non-coincident), linia prosta, do której nieskończona gałąź krzywej zbliża się w nieskończoność, na przykład asymptota hiperboli. ... Ilustrowany słownik encyklopedyczny
ASYMPTOTA- kobieta, geom. linia prosta, zawsze zbliżająca się do krzywej (hiperbola), ale nigdy z nią nie zbiegająca. Przykład, aby to wyjaśnić: jeśli jakakolwiek liczba zostanie podzielona na pół, to zmniejszy się do nieskończoności, ale nigdy nie osiągnie zera ... ... Słownik wyjaśniający Dahla
asymptota- rzeczownik, liczba synonimów: 1 linia (182) Słownik synonimów ASIS. V.N. Triszyn. 2013 ... Słownik synonimów
Asymptota- (od greckich słów: a, słońce, piptw) niedopasowane. Asymptota to linia, która, będąc kontynuowana w nieskończoność, zbliża się do danej zakrzywionej linii lub jej części, tak że odległość między liniami wspólnymi staje się mniejsza ... ...
Asymptota- powierzchnia to linia prosta, która przecina powierzchnię co najmniej w dwóch nieskończenie odległych punktach ... Encyklopedia Brockhaus i Efron
ASYMPTOTA- (asymptota) Wartość, do której ta funkcja dąży podczas zmiany argumentu (argumentu), ale nie osiąga jej dla żadnej skończonej wartości argumentu. Na przykład, jeśli całkowity koszt produkcji x jest podany przez funkcję TC = a + bx, gdzie a i b są stałymi ... Słownik ekonomiczny
Asymptota- linia prosta, do której zmierza krzywa jakiejś funkcji (nigdy jej nie osiąga), mająca nieskończoną gałąź, gdy jej argument rośnie lub maleje w nieskończoność. Na przykład w funkcji: y = c + 1 / x, wartość y zbliża się od ... ... Słownik ekonomii i matematyki
- Pojęcie asymptot
Jednym z ważnych kroków w kreśleniu funkcji jest znalezienie asymptot. Niejednokrotnie spotykaliśmy się z asymptotami: podczas kreślenia wykresów funkcji, y = tgx, y = ctgx... Zdefiniowaliśmy je jako linie, do których „dąży” wykres funkcji, ale nigdy ich nie przecina. Czas podać dokładną definicję asymptot.
Asymptoty są trzech typów: pionowe, poziome i ukośne. Na rysunku asymptoty są zwykle oznaczone liniami przerywanymi.
Rozważmy następujący sztucznie wykreślony wykres funkcji (ryc. 16.1), na przykład wszystkie typy asymptot są wyraźnie widoczne:
Podajmy definicję dla każdego typu asymptoty:
1. Bezpośrednie x = a zwany pionowa asymptota działa, jeśli.
2. Bezpośrednie y = c zwany asymptota pozioma działa, jeśli.
3. Bezpośredni y = kx + b zwany asymptota ukośna działa, jeśli.
Geometrycznie definicja asymptoty ukośnej oznacza, że jako → ∞ wykres funkcji zbliża się dowolnie do linii prostej y = kx + b, tj. są prawie takie same. Różnica praktycznie identycznych wyrażeń zmierza do zera.
Zauważ, że asymptoty poziome i ukośne są brane pod uwagę tylko pod warunkiem → ∞. Czasami rozróżnia się je na asymptoty poziome i ukośne na → + ∞ i → -∞.
- Algorytm znajdowania asymptot
Do znalezienia asymptot można użyć następującego algorytmu:
Może istnieć jedna asymptota pionowa, kilka lub wcale.
- Jeśli c jest liczbą, to y = c- asymptota pozioma;
- Jeśli c jest nieskończonością, to nie ma asymptot poziomych.
Jeśli funkcja jest stosunkiem dwóch wielomianów, to jeśli funkcja ma asymptoty poziome, nie będziemy szukać asymptot ukośnych - nie są.
Rozważ przykłady znajdowania asymptot funkcji:
Przykład 16.1. Znajdź asymptoty krzywej.
Rozwiązanie NS-1≠0; NS≠1.
Sprawdź, czy linia prosta x = 1 przez pionową asymptotę. Aby to zrobić, obliczamy granicę funkcji w punkcie x = 1: .
x = 1 - pionowa asymptota.
z= .
z= =. Bo z= 2 (liczba), to y = 2- asymptota pozioma.
Ponieważ funkcja jest stosunkiem wielomianów, w obecności asymptot poziomych twierdzimy, że nie ma asymptot ukośnych.
x = 1 i asymptota pozioma r = 2. Dla jasności wykres tej funkcji pokazano na ryc. 16.2.
Przykład 16.2... Znajdź asymptoty krzywej.
Rozwiązanie... 1. Znajdźmy dziedzinę definicji funkcji: NS-2≠0; NS≠2.
Sprawdź, czy linia prosta x = 2 przez pionową asymptotę. Aby to zrobić, obliczamy granicę funkcji w punkcie x = 2: .
Mamy to, dlatego x = 2 - asymptota pionowa.
2. Aby wyszukać asymptoty poziome, znajdujemy: z= .
Ponieważ w limicie pojawia się niepewność, użyjemy reguły L'Hôpitala: z= =. Bo z Jest nieskończoność, to nie ma asymptot poziomych.
3. Aby wyszukać asymptoty ukośne, znajdujemy:
Otrzymaliśmy niepewność formy, korzystamy z reguły L'Hôpitala: = = 1. Czyli 1. Znajdź b według wzoru: .
b = = =
Zrozumiałeś b = 2. Wtedy y = kx + b - asymptota ukośna. W naszym przypadku wygląda to tak: y = x + 2.
|
Pytania testowe:
Wykład 17. OGÓLNY SCHEMAT FUNKCJI STUDIOWANIA I BUDOWY GRAFIKI
W tym wykładzie podsumujemy cały wcześniej przestudiowany materiał. Ostatecznym celem naszej długiej podróży jest możliwość zbadania dowolnej analitycznie zdefiniowanej funkcji i zbudowania jej wykresu. Ważnymi ogniwami naszych badań będzie badanie funkcji ekstremów, wyznaczanie przedziałów monotoniczności, wypukłości i wklęsłości wykresu, poszukiwanie punktów przegięcia, asymptoty wykresu funkcji.
Biorąc pod uwagę wszystkie powyższe aspekty, przedstawiamy badanie funkcji i schemat kreślenia .
1. Znajdź dziedzinę funkcji.
2. Zbadaj funkcję parzystości parzystość-nieparzysta:
Jeżeli, to funkcja jest parzysta (wykres funkcji parzystej jest symetryczny względem osi OU);
· Jeśli, to funkcja jest nieparzysta (wykres funkcji nieparzystej jest symetryczny względem początku);
· W przeciwnym razie funkcja nie jest ani parzysta, ani nieparzysta.
3. Zbadaj funkcję okresowości (spośród funkcji, które badamy, tylko funkcje trygonometryczne mogą być okresowe).
4. Znajdź punkty przecięcia wykresu funkcji z osiami współrzędnych:
· Oh: w= 0 (rozwiązujemy równanie tylko wtedy, gdy możemy użyć znanych nam metod);
· OU: NS=0.
5. Znajdź pierwszą pochodną funkcji i punkty krytyczne pierwszego rodzaju.
6. Znajdź przedziały monotoniczności i ekstrema funkcji.
7. Znajdź drugą pochodną funkcji i punkty krytyczne drugiego rodzaju.
8. Znajdź przedziały wypukłości-wklęsłości wykresu funkcji i punktu przegięcia.
9. Znajdź asymptoty wykresu funkcji.
10. Zbuduj wykres funkcji. Podczas budowania należy wziąć pod uwagę przypadki możliwego położenia grafu w pobliżu asymptot :
11. W razie potrzeby wybierz punkty kontrolne, aby uzyskać dokładniejszą konstrukcję.
Rozważ schemat badania funkcji i kreślenia jej wykresu na konkretnych przykładach:
Przykład 17.1... Wykreśl funkcję.
Rozwiązanie... 1. Ta funkcja jest zdefiniowana na całej linii liczbowej z wyjątkiem NS= 3, ponieważ w tym momencie znika mianownik.
2. Aby określić parzystość i nieparzystość funkcji, znajdujemy:
Widzimy to i dlatego funkcja nie jest ani parzysta, ani nieparzysta.
3. Funkcja jest nieokresowa.
4. Znajdź punkty przecięcia z osiami współrzędnych. Aby znaleźć punkt przecięcia z osią Oh zaakceptować w= 0. Otrzymujemy równanie:. Tak więc punkt (0; 0) jest punktem przecięcia z osiami współrzędnych.
5. Znajdź pochodną funkcji zgodnie z zasadą różniczkowania ułamka: = = = =.
Aby znaleźć punkty krytyczne, znajdujemy punkty, w których pochodna funkcji jest równa 0 lub nie istnieje.
Jeśli = 0, zatem. Iloczyn jest wtedy równy 0, gdy przynajmniej jeden z czynników jest równy 0: lub.
NS-3) 2 to 0, tj. nie istnieje dla NS=3.
Tak więc funkcja ma trzy punkty krytyczne pierwszego rodzaju:; ; ...
6. Na osi liczbowej zaznacz punkty krytyczne pierwszego rodzaju i zaznacz punkt przebitym, ponieważ funkcja nie jest w nim zdefiniowana.
Na każdym przedziale umieszczamy znaki pochodnej =:
|
|
Na przedziałach, gdzie pierwotna funkcja rośnie (w (-∞; 0]), gdzie - maleje (w).
Kropka NS= 0 to maksymalny punkt funkcji. Aby znaleźć maksimum funkcji, znajdujemy wartość funkcji w punkcie 0:.
Kropka NS= 6 to minimalny punkt funkcji. Aby znaleźć minimum funkcji, znajdujemy wartość funkcji w punkcie 6:.
Wyniki badań można wpisać w tabeli. Liczba wierszy w tabeli jest ustalona na cztery, a liczba kolumn zależy od badanej funkcji. W komórkach pierwszego wiersza wprowadza się kolejno przedziały, w których punkty krytyczne dzielą dziedzinę funkcji, w tym same punkty krytyczne. Aby uniknąć błędów podczas konstrukcji, w tabeli można pominąć punkty, które nie należą do obszaru definicji.
W drugim wierszu tabeli w każdym z rozpatrywanych przedziałów umieszczono znaki pochodnej, a w punktach krytycznych wartość pochodnej. Zgodnie ze znakami pochodnej funkcji, w trzecim wierszu zaznaczono przedziały wzrostu, spadku i ekstrema funkcji.
Ostatni wiersz służy do wskazania maksimum i minimum funkcji.
| NS | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f (x) | |||||||
| wnioski | maks | min |
7. Znajdź drugą pochodną funkcji jako pochodną pierwszej pochodnej: = =
Wyjmijmy w liczniku NS-3 poza nawiasami i wykonaj redukcję:
Podajmy podobne terminy w liczniku:.
Znajdźmy punkty krytyczne drugiego rodzaju: punkty, w których druga pochodna funkcji wynosi zero lub nie istnieje.
0 jeśli = 0. Ten ułamek nie może być równy zero, dlatego nie ma punktów, w których druga pochodna funkcji jest równa zero.
Nie istnieje, jeśli mianownik ( NS-3) 3 to 0, tj. nie istnieje dla NS= 3. :Oh , OU, pochodzenie, jednostki miary dla każdej osi.
Przed wykreśleniem wykresu funkcji musisz:
· Rysuj asymptoty liniami przerywanymi;
· Zaznacz punkty przecięcia z osiami współrzędnych;
|
· Wykorzystując uzyskane dane o przedziałach wzrostu, spadku, wypukłości i wklęsłości, zbuduj wykres funkcji. Gałęzie wykresu powinny „zbiegać” do asymptot, ale ich nie przecinać.
· Sprawdź, czy wykres funkcji odpowiada badaniu: jeśli funkcja jest parzysta lub nieparzysta, to czy obserwuje się symetrię; czy przedziały wzrostu i spadku, wypukłości i wklęsłości, punkty przegięcia odpowiadają teoretycznie tym znalezionym.
11. Aby uzyskać dokładniejszą konstrukcję, możesz wybrać kilka punktów kontrolnych. Na przykład znajdźmy wartości funkcji w punktach -2 i 7:
Dostosujmy wykres, biorąc pod uwagę punkty kontrolne.
Pytania testowe:
- Jaki jest algorytm wykreślania funkcji?
- Czy funkcja może mieć ekstremum w punktach poza dziedziną definicji?
ROZDZIAŁ 3. 3. CAŁKOWITE OBLICZANIE FUNKCJI
Nie zabraknie również zadań do samodzielnego rozwiązania, na które będzie można zobaczyć odpowiedzi.
Pojęcie asymptot
Jeśli najpierw wykreślisz asymptoty krzywej, w wielu przypadkach konstrukcja wykresu funkcji jest ułatwiona.
Losy asymptoty są pełne tragedii. Wyobraź sobie, jak to jest: przez całe życie iść w linii prostej do upragnionego celu, zbliżyć się do niego jak najbliżej, ale nigdy go nie osiągnąć. Na przykład, aby dążyć do połączenia swojej ścieżki życiowej ze ścieżką pożądanej osoby, w pewnym momencie zbliżyć się do niej prawie blisko, ale nawet jej nie dotknąć. Albo staraj się zarobić miliard, ale zanim osiągniesz ten cel i wejdziesz do Księgi Rekordów Guinnessa, w twoim przypadku setki centów to za mało. Itp. Tak jest z asymptotą: nieustannie dąży do osiągnięcia krzywej wykresu funkcji, zbliża się do niej na minimalną możliwą odległość, ale jej nie dotyka.
Definicja 1. Asymptoty to linie proste, do których wykres funkcji zbliża się tak blisko, jak to pożądane, gdy zmienna dąży do plus nieskończoności lub minus nieskończoności.
Definicja 2. Prostą nazywamy asymptotą wykresu funkcji, jeśli odległość od punktu zmiennej m wykres funkcji do tej prostej dąży do zera przy nieograniczonej odległości punktu m od początku wzdłuż jakiejś gałęzi wykresu funkcji.
Istnieją trzy rodzaje asymptot: pionowa, pozioma i ukośna.
Asymptoty pionowe
Pierwszą rzeczą, którą należy wiedzieć o asymptotach pionowych: są one równoległe do osi Oy .
Definicja... Prosty x = a jest pionowa asymptota wykresu funkcji jeśli punkt x = a jest punkt przerwania drugiego rodzaju dla tej funkcji.
Z definicji wynika, że linia prosta x = a jest pionową asymptotą wykresu funkcji F(x), jeżeli spełniony jest co najmniej jeden z poniższych warunków:
W tym przypadku funkcja F(x) nie można w ogóle zdefiniować, odpowiednio dla x ≥ a oraz x ≤ a .
Komentarz:
Przykład 1. Wykres funkcji tak= ln x ma pionową asymptotę x= 0 (tj. pokrywające się z osią Oy) na granicy dziedziny definicji, ponieważ granica funkcji przy x dążącym do zera po prawej stronie jest równa minus nieskończoność:
(rys. powyżej).
siebie, a następnie zobacz rozwiązania
Przykład 2. Znajdź asymptoty wykresu funkcji.
Przykład 3. Znajdź asymptoty wykresu funkcji
Asymptoty poziome
Pierwszą rzeczą, którą należy wiedzieć o asymptotach poziomych: są one równoległe do osi Wół .
Jeśli (granica funkcji jako argument ma tendencję do plus lub minus nieskończoność jest równa pewnej wartości b), następnie tak = b – asymptota pozioma krzywy tak = F(x ) (w prawo, gdy x dąży do plus nieskończoności, w lewo, gdy x dąży do minus nieskończoności, i dwustronny, jeśli granice są równe, gdy x dąży do plus lub minus nieskończoności).
Przykład 5. Wykres funkcji
w a> 1 ma lewą poziomą asympotę tak= 0 (tj. pokrywające się z osią Wół), ponieważ granica funkcji jako „x” dąży do minus nieskończoności jest równa zeru:
Krzywa nie ma prawej poziomej asymptoty, ponieważ granica funkcji jako „x” ma tendencję do plus nieskończoność jest równa nieskończoności:
Asymptoty ukośne
Asymptoty pionowe i poziome, które rozważaliśmy powyżej, są równoległe do osi współrzędnych, dlatego do ich skonstruowania potrzebowaliśmy tylko pewnej liczby - punktu na osi odciętej lub rzędnej, przez którą przechodzi asymptota. Dla ukośnej asymptoty potrzeba więcej - nachylenie k, który pokazuje kąt nachylenia prostej oraz wyraz swobodny b, który pokazuje, jak bardzo linia znajduje się powyżej lub poniżej początku. Ci, którzy nie mieli czasu zapomnieć o geometrii analitycznej, a od niej - równaniach prostej, zauważą, że dla ukośnej asymptoty znajdują równanie nachylenia... O istnieniu asymptoty ukośnej decyduje następujące twierdzenie, na podstawie którego znajdują się wspomniane współczynniki.
Twierdzenie. Do krzywej tak = F(x) miał asymptotę tak = kx + b , konieczne i wystarczające jest istnienie skończonych granic k oraz b rozważanej funkcji jako zmiennej tendencje x do plus nieskończoności i minus nieskończoności:
(1)
(2)
Liczby znalezione w ten sposób k oraz b i są współczynnikami asymptoty ukośnej.
W pierwszym przypadku (ponieważ x dąży do plus nieskończoności) uzyskuje się prawą asymptotę ukośną, w drugim (ponieważ x dąży do minus nieskończoności) lewą. Prawa asymptota skośna jest pokazana na ryc. od dołu.
Przy znajdowaniu równania asymptoty ukośnej należy wziąć pod uwagę tendencję x zarówno do plus nieskończoności, jak i minus nieskończoności. Dla niektórych funkcji, na przykład dla wymiernej ułamkowej, granice te pokrywają się, jednak dla wielu funkcji granice te są różne i tylko jedna z nich może istnieć.
Jeśli granice pokrywają się z x dążącym do plus nieskończoności i do minus nieskończoności, linia prosta tak = kx + b jest dwustronną asymptotą krzywej.
Jeśli przynajmniej jedna z granic określających asymptotę tak = kx + b , nie istnieje, to wykres funkcji nie ma asymptoty ukośnej (ale może mieć pionową).
Łatwo zauważyć, że pozioma asymptota tak = b jest szczególnym przypadkiem ukośnego tak = kx + b w k = 0 .
Dlatego jeśli w jakimś kierunku krzywa ma poziomą asymptotę, to w tym kierunku nie ma ukośnej i odwrotnie.
Przykład 6. Znajdź asymptoty wykresu funkcji
Rozwiązanie. Funkcja jest zdefiniowana na całej linii liczbowej, z wyjątkiem x= 0, tj.
Dlatego w punkcie przerwania x= 0 krzywa może mieć pionową asymptotę. Rzeczywiście, granica funkcji, gdy x dąży do zera od lewej, jest równa plus nieskończoności:
W konsekwencji, x= 0 - pionowa asymptota wykresu tej funkcji.
Wykres tej funkcji nie ma poziomej asymptoty, ponieważ granica funkcji, gdy x dąży do plus nieskończoności, jest równa plus nieskończoności:
Dowiedzmy się o obecności ukośnej asymptoty:
Masz skończone granice k= 2 i b= 0. Prosty tak = 2x jest dwustronną ukośną asymptotą wykresu tej funkcji (rys. wewnątrz przykładu).
Przykład 7. Znajdź asymptoty wykresu funkcji
Rozwiązanie. Funkcja ma jeden punkt przerwania x= -1. Obliczamy granice jednostronne i określamy rodzaj nieciągłości:
Wniosek: x= −1 jest punktem nieciągłości drugiego rodzaju, stąd prosta x= -1 to pionowa asymptota wykresu tej funkcji.
Poszukujemy asymptot ukośnych. Ponieważ ta funkcja jest wymierna ułamkowo, granice dla i dla będą się pokrywać. W ten sposób znajdujemy współczynniki do podstawienia do równania prostej - asymptota ukośna:
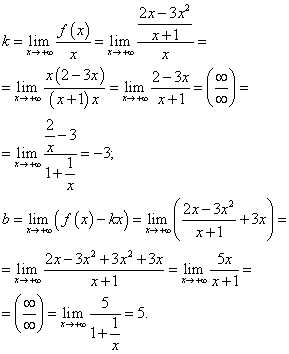
Podstawiając znalezione współczynniki do równania prostej ze spadkiem, otrzymujemy równanie ukośnej asymptoty:
tak = −3x + 5 .
Na rysunku wykres funkcji zaznaczono kolorem bordowym, a asymptoty kolorem czarnym.
Przykład 8. Znajdź asymptoty wykresu funkcji
Rozwiązanie. Ponieważ ta funkcja jest ciągła, jej wykres nie ma pionowych asymptot. Poszukujemy asymptot ukośnych:
.
Zatem wykres tej funkcji ma asymptotę tak= 0 w i nie ma asyptoty w.
Przykład 9. Znajdź asymptoty wykresu funkcji
Rozwiązanie. Najpierw szukamy asymptot pionowych. Aby to zrobić, znajdź domenę funkcji. Funkcja jest zdefiniowana, gdy nierówność jest spełniona i jednocześnie. Znak zmienny x pasuje do znaku. Dlatego rozważ równoważną nierówność. Z tego otrzymujemy domenę funkcji: 
... Asymptota pionowa może znajdować się tylko na granicy dziedziny definicji funkcji. Jednak x= 0 nie może być pionową asymptotą, ponieważ funkcja jest zdefiniowana dla x = 0
.
Rozważmy limit dla praworęcznych na (limit dla leworęcznych nie istnieje):
.
Kropka x= 2 jest punktem nieciągłości drugiego rodzaju, stąd prosta x= 2 - pionowa asymptota wykresu tej funkcji.
Poszukujemy asymptot ukośnych:
Więc, tak = x+ 1 - ukośna asymptota wykresu tej funkcji przy godz. Poszukujemy asymptoty ukośnej dla:
Więc, tak = −x − 1 jest ukośną asymptotą przy.
Przykład 10. Znajdź asymptoty wykresu funkcji
Rozwiązanie. Funkcja ma zakres 
... Ponieważ pionowa asymptota wykresu tej funkcji może znajdować się tylko na granicy dziedziny definicji, jednostronne granice funkcji znajdują się na.
