Найти все асимптоты графика функции. Асимптоты графика функции. Вертикальные асимптоты графика функции
Асимптоты графика функции
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции . Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций , а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен;-) …стоп-стоп, вы куда? Пределы – это легко!
Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций , и сейчас тема получает детальное рассмотрение.
Итак, что такое асимптота?
Представьте переменную точку , которая «ездит» по графику функции. Асимптота – это прямая , к которой неограниченно близко приближается график функции при удалении его переменной точки в бесконечность.
Примечание : определение содержательно, если вам необходима формулировка в обозначениях математического анализа, пожалуйста, обратитесь к учебнику.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные асимптоты
, которые задаются уравнением вида , где «альфа» – действительное число. Популярная представительница определяет саму ось ординат,
с приступом лёгкой тошноты вспоминаем гиперболу .
2) Наклонные асимптоты традиционно записываются уравнением прямой с угловым коэффициентом . Иногда отдельной группой выделяют частный случай – горизонтальные асимптоты . Например, та же гипербола с асимптотой .
Резво пошло-поехало, ударим по теме короткой автоматной очередью:
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции . Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит ?
Вертикальные асимптоты графика функции
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание : обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один
из односторонних пределов 
бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции
. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: и ось ординат (см. Графики и свойства элементарных функций
).
Из вышесказанного также следует очевидный факт: если функция непрерывна на , то вертикальные асимптоты отсутствуют . На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай – горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше двух наклонных асимптот . Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при , а график арктангенса при – двумя такими асимптотами, причём различными.
Когда график и там и там сближается с единственной наклонной асимптотой, то «бесконечности» принято объединять под единой записью . Например, …правильно догадались: .
Общее практическое правило :
Если существуют два конечных
предела 
, то прямая является наклонной асимптотой графика функции при . Если хотя бы один
из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
Примечание : формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Покажем, что у параболы нет наклонных асимптот:
Предел бесконечен, значит, наклонная асимптота отсутствует. Заметьте, что в нахождении предела 
необходимость отпала, поскольку ответ уже получен.
Примечание
: если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока
о бесконечно малых функциях
, где я рассказал, как правильно интерпретировать данные знаки.
Очевидно, что у любой квадратичной, кубической функции, многочлена 4-й и высших степеней также нет наклонных асимптот.
А теперь убедимся, что при у графика тоже нет наклонной асимптоты. Для раскрытия неопределённости используем правило Лопиталя
:
, что и требовалось проверить.
При функция неограниченно растёт, однако не существует такой прямой, к которой бы её график приближался бесконечно близко .
Переходим к практической части урока:
Как найти асимптоты графика функции?
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти асимптоты графика функции
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв
, а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье Непрерывность функции. Точки разрыва
. В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число
:
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого – они ПОМОГАЮТ ПОНЯТЬ, КАК
расположен график функции и построить его КОРРЕКТНО
. Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен
, значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен
.
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты
можно пользоваться упрощенной формулой
:
Если существует конечный предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста
, а значит, искомый предел будет конечным: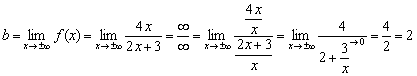
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции
, то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции
, и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдена по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва
, поэтому нужно проверить, обращается ли знаменатель в ноль. Решим квадратное уравнение
:
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители
:
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде 
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию 
, то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка – в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая – через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен
, поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность»
приводим выражение к общему знаменателю: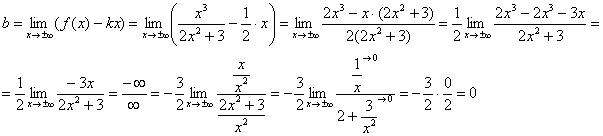
Второй предел тоже конечен
, следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции 
бесконечно близко
приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .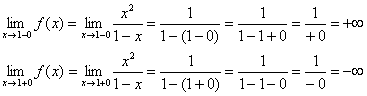
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ
: 
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше – наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Пример 11
Исследовать график функции на наличие асимптот
Решение
: очевидно, что 
, поэтому рассматриваем только правую полуплоскость, где есть график функции.
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопиталя
мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: 
(см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ
:
, если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
- (от греч. a отриц. част., и symptotos совпадающий вместе). Прямая линия, постоянно приближающаяся к кривой и встречающаяся с ней только в бесконечности. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. АСИМПТОТА от… … Словарь иностранных слов русского языка
АСИМПТОТА - (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы … Современная энциклопедия
АСИМПТОТА - (от греч. asymptotos несовпадающий) кривой с бесконечной ветвью прямая, к которой эта ветвь неограниченно приближается, напр., асимптота гиперболы … Большой Энциклопедический словарь
асимптота - Прямая линия, к которой постепенно приближается кривая. асимптота Прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или … Справочник технического переводчика
Асимптота - (от греческого asymptotos несовпадающая), прямая, к которой бесконечная ветвь кривой приближается неограниченно, например асимптота гиперболы. … Иллюстрированный энциклопедический словарь
АСИМПТОТА - жен., геом. прямая черта, вечно близящаяся к кривой (гиперболе), но никогда с нею не сходящаяся. Пример, для объяснения этого: если какое либо число все делить пополам, то оно будет умаляться до бесконечности, но никогда не сделается нулем.… … Толковый словарь Даля
асимптота - сущ., кол во синонимов: 1 линия (182) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Асимптота - (от греч. слов: a, sun, piptw) несовпадающая. Подасимптотой подразумевается такая линия, которая, будучи неопределеннопродолжена, приближается к данной кривой линии или к некоторой ее частитак, что расстояние между общими линиями делается менее… …
Асимптота - поверхности называется прямая линия, пересекающаяповерхность по крайней мере в двух бесконечно удаленных точках … Энциклопедия Брокгауза и Ефрона
АСИМПТОТА - (asymptote) Значение, к которому стремится данная функция при изменении аргумента (argument), но не достигает его ни при одном конечном значении аргумента. Например, если общая стоимость выпуска х задается функцией ТС=а+bх, где а и b – константы … Экономический словарь
Асимптота - прямая, к которой стремится (никогда не достигая ее), имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент неограниченно возрастает или уменьшается. Например, в функции: y = c + 1/x значение y приближается с… … Экономико-математический словарь
- Понятие асимптот
Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций , y=tgx , y=сtgx . Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.
Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.
Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:
Дадим определение каждому виду асимптот:
1. Прямая х=а называется вертикальной асимптотой функции , если .
2. Прямая у=с называется горизонтальной асимптотой функции , если .
3. Прямая у=kx+b называется наклонной асимптотой функции , если .
Геометрически определение наклонной асимптоты означает, что при →∞ график функции сколь угодно близко подходит к прямой у=kx+b , т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.
Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии →∞. Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.
- Алгоритм поиска асимптот
Для поиска асимптот можно использовать следующий алгоритм:
Вертикальных асимптот может быть одна, несколько или не быть совсем.
- Если с – число, то у=с – горизонтальная асимптота;
- Если с – бесконечность, то горизонтальных асимптот нет.
Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.
Рассмотрим примеры нахождения асимптот функции:
Пример 16.1. Найдите асимптоты кривой .
Решение х -1≠0; х ≠1.
Проверим, является ли прямая х= 1 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 1: .
х= 1 - вертикальная асимптота.
с = .
с = = . Т.к. с =2 (число), то у=2 – горизонтальная асимптота.
Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.
х= 1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.
Пример 16.2 . Найдите асимптоты кривой .
Решение . 1. Найдем область определения функции: х -2≠0; х ≠2.
Проверим, является ли прямая х= 2 вертикальной асимптотой. Для этого вычислим предел функции в точке х= 2: .
Получили, что , следовательно, х= 2 - вертикальная асимптота.
2. Для поиска горизонтальных асимптот находим : с = .
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с = = . Т.к. с – бесконечность, то горизонтальных асимптот нет.
3. Для поиска наклонных асимптот находим :
Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .
b= = =
Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.
|
Контрольные вопросы:
Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА
В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.
С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика .
1. Найти область определения функции.
2. Исследовать функцию на четность-нечетность:
· если , то функция четная (график четной функции симметричен относительно оси Оу );
· если , то функция нечетная (график нечетной функции симметричен относительно начала координат);
· в противном случае функция ни четная, ни нечетная.
3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).
4. Найти точки пересечения графика функции с осями координат:
· Ох : у =0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);
· Оу : х =0.
5. Найти первую производную функции и критические точки первого рода.
6. Найти интервалы монотонности и экстремумы функции.
7. Найти вторую производную функции и критические точки второго рода.
8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.
9. Найти асимптоты графика функции.
10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот :
11. При необходимости выбрать контрольные точки для более точного построения.
Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:
Пример 17.1 . Постройте график функции .
Решение . 1. Данная функция определена на всей числовой прямой за исключением х =3, т.к. в этой точке знаменатель обращается в ноль.
2. Для определения четности и нечетности функции найдем :
Видим, что и , следовательно, функция ни четная, ни нечетная.
3. Функция непериодическая.
4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у =0. Получим уравнение: . Итак, точка (0; 0) – точка пересечения с осями координат.
5. Найдем производную функции по правилу дифференцирования дроби: = = = = .
Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.
Если =0, следовательно, . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: или .
х -3) 2 равен 0, т.е. не существует при х =3.
Итак, функция имеет три критические точки первого рода: ; ; .
6. На числовой оси отметим критические точки первого рода, причем точку отмечаем выколотой точкой, т.к. в ней функция не определена.
Расставляем знаки производной = на каждом промежутке:
|
|
На промежутках, где , исходная функция возрастает (при (-∞;0] ), где - убывает (при ).
Точка х =0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .
Точка х =6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .
Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.
Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.
Последняя строка служит для обозначения максимума и минимума функции.
| х | (-∞;0) | (0;3) | (3;6) | (6;+ ∞) | |||
| + | - | - | + | ||||
| f(x) | |||||||
| Выводы | max | min |
7. Найдем вторую производную функции как производную от первой производной: = =
Вынесем в числителе х -3 за скобки и выполним сокращение:
Приведем в числителе подобные слагаемые: .
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.
0, если =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.
Не существует, если знаменатель (х -3) 3 равен 0, т.е. не существует при х =3. :Ох , Оу , начало отсчета, единицы измерения по каждой оси.
Прежде чем строить график функции, нужно:
· провести асимптоты пунктирными линиями;
· отметить точки пересечения с осями координат;
|
· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.
· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.
11. Для более точного построения можно выбрать несколько контрольных точек. Например, найдем значения функции в точках -2 и 7:
Корректируем график с учетом контрольных точек.
Контрольные вопросы:
- Каков алгоритм построения графика функции?
- Может ли функция иметь экстремум в точках, не принадлежащих области определении?
ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие асимптоты
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy .
Определение . Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:
При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .
Замечание:
Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Горизонтальные асимптоты
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox .
Если (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ), то y = b – горизонтальная асимптота кривой y = f (x ) (правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности, и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении "икса" к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении "икса" к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число - точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше - угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё - уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
Заключение: x = −1 - точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция - дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой - наклонной асимптоты:
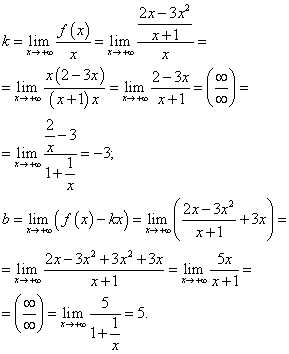
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5 .
На рисунке график функции обозначен бордовым цветом, а асимптоты - чёрным.
Пример 8. Найти асимптоты графика функции
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения
функции. Функция определена, когда выполняется неравенство и
при этом . Знак переменной
x
совпадает со знаком .
Поэтому рассмотрим эквивалентное неравенство .
Из этого получаем область определения функции: 
.
Вертикальная асимптота может быть только на границе области определения функции. Но
x
= 0
не может быть вертикальной асимптотой, так как
функция определена при x
= 0
.
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 - точка разрыва второго рода, поэтому прямая x = 2 - вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 - наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 - наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения 
.
Так как вертикальная асимптота графика этой функции может быть только на границе области определения,
найдём односторонние пределы функции при .
