дома > Идеи > Како да се реши логаритамски израз. Пресметка на логаритми, примери, решенија


Како да се реши логаритамски израз. Пресметка на логаритми, примери, решенија




Дефиниција на логаритам

Логаритмот од b до основата a е експонентот до кој мора да се подигне a за да се добие b.

Број дво математиката вообичаено е да се означи границата до која се стреми изразот

Број де ирационален број - број неспоредлив со еден, не може точно да се изрази ниту како цел број ниту како дропка рационаленброј.

Писмо д- прва буква Латински збор изложувач- да се покаже, па оттука и името во математиката експоненцијален- експоненцијална функција.

Број дшироко користен во математиката, и во сите науки кои на еден или друг начин користат математички пресметки за своите потреби.

Логаритми. Својства на логаритмите

Дефиниција: Логаритмот на позитивен број b на неговата основа е експонентот c на кој мора да се подигне бројот a за да се добие бројот b.

Основи логаритамски идентитет:

7) Формула за преселба во нова база:

lna = log e a, e ≈ 2,718…

Задачи и тестови на тема „Логаритми. Својства на логаритмите“

  • Логаритми - Важни теми за прегледување на Единствениот државен испит по математика

За успешно завршување на задачите на оваа тема, мора да ја знаете дефиницијата за логаритам, својствата на логаритмите, основниот логаритамски идентитет, дефинициите за децимални и природни логаритми. Главните типови на проблеми на оваа тема се проблеми кои вклучуваат пресметување и трансформација на логаритамски изрази. Да го разгледаме нивното решение користејќи ги следните примери.

Решение:Користејќи ги својствата на логаритмите, добиваме

Решение:Користејќи ги својствата на степените, добиваме

1) (2 2) дневник 2 5 =(2 дневник 2 5) 2 =5 2 =25

Својства на логаритми, формулации и докази.

Логаритмите имаат голем број на карактеристични својства. Во оваа статија ќе ги разгледаме главните својства на логаритми. Овде ќе ги дадеме нивните формулации, ќе ги запишеме својствата на логаритмите во форма на формули, ќе покажеме примери за нивната примена, а исто така ќе обезбедиме доказ за својствата на логаритмите.

Навигација на страницата.

Основни својства на логаритмите, формули

За полесно запомнување и користење, ајде да замислиме основни својства на логаритмитево форма на листа на формули. Во следниот пасус ќе ги дадеме нивните формулации, докази, примери за употреба и потребни објаснувања.

  • Својство на логаритамот на единство: log a 1=0 за кое било a>0, a≠1.
  • Логаритм на број, еднаква на основата: log a a=1 за a>0, a≠1.
  • Својство на логаритамот на моќноста на основата: log a a p =p, каде што a>0, a≠1 и p е секој реален број.
  • Логаритам на производот од два позитивни броја: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
    и својството на логаритамот на производот од n позитивни броеви: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, ..., x n >0.
  • Својство на логаритам на количник: , каде што a>0, a≠1, x>0, y>0.
  • Логаритам на моќноста на број: log a b p =p·log a |b| , каде што a>0, a≠1, b и p се броеви такви што степенот b p има смисла и b p >0.
  • Последица: , каде a>0, a≠1, n - природен број, поголемо од еден, b>0.
  • Заклучок 1: , a>0, a≠1, b>0, b≠1.
  • Заклучок 2: , a>0 , a≠1 , b>0 , p и q се реални броеви, q≠0 , особено за b=a имаме .

    • Формулации и докази за својства

    Продолжуваме со формулација и докажување на пишаните својства на логаритмите. Сите својства на логаритмите се докажани врз основа на дефиницијата на логаритмот и основниот логаритамски идентитет што произлегува од него, како и својствата на степенот.

    Да почнеме со својства на логаритмот на еден. Неговата формулација е како што следува: логаритамот на единство е еднаков на нула, т.е. логирајте 1=0за кое било a>0, a≠1. Доказот не е тежок: бидејќи a 0 =1 за кој било a ги задоволува горенаведените услови a>0 и a≠1, тогаш логот за еднаквост a 1=0 што треба да се докаже следи веднаш од дефиницијата на логаритамот.

    Да дадеме примери за примена на разгледуваното својство: log 3 1=0, log1=0 и .

    Ајде да преминеме на следниот имот: логаритамот на број еднаков на основата е еднаков, тоа е, log a a=1за a>0, a≠1. Навистина, бидејќи a 1 =a за кое било a, тогаш по дефиниција на логаритамот log a a=1.

    Примери за користење на ова својство на логаритми се еднаквостите log 5 5=1, log 5.6 5.6 и lne=1.

    Логаритмот на моќта на број еднаков на основата на логаритамот е еднаков на експонентот. Ова својство на логаритмот одговара на формулата на формата log a a p =p, каде што a>0, a≠1 и p – кој било реален број. Ова својство произлегува директно од дефиницијата на логаритамот. Забележете дека ви овозможува веднаш да ја означите вредноста на логаритмот, ако е можно да се претстави бројот под знакот за логаритам како моќност на основата, ќе зборуваме повеќе за ова во написот за пресметување логаритми.

    На пример, log 2 2 7 =7, log10 -4 =-4 и .

    Логаритам на производот од два позитивни броја x и y е еднаков на производот од логаритмите на овие броеви: log a (x y)=log a x+log a y, a>0, a≠1. Да го докажеме својството на логаритмот на производот. Поради својствата на степенот a log a x+log a y =a log a x ·a log a y, и бидејќи според главниот логаритамски идентитет log a x =x и лог a y =y, тогаш лог a x ·a log a y =x· y. Така, лог a x+log a y =x·y, од кој, според дефиницијата на логаритам, следи еднаквоста што се докажува.

    Да покажеме примери за користење на својството на логаритам на производ: log 5 (2 3)=log 5 2+log 5 3 и .

    Својството на логаритмот на производ може да се генерализира на производот на конечен број n од позитивни броеви x 1 , x 2 , …, x n како log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Оваа еднаквост може да се докаже без проблеми со користење на методот на математичка индукција.

    На пример, природниот логаритам на производот може да се замени со збир од три природни логаритми од броевите 4, e и.

    Логаритам на количник на два позитивни броја x и y е еднаква на разликата помеѓу логаритмите на овие броеви. Својството на логаритмот на количникот одговара на формула на формата , каде што a>0, a≠1, x и y се некои позитивни броеви. Се докажува валидноста на оваа формула како и формулата за логаритам на производ: бидејќи , тогаш по дефиниција на логаритам .

    Еве пример за користење на ова својство на логаритмот: .

    Ајде да продолжиме на својство на логаритмот на моќноста. Логаритмот на степен е еднаков на производот на експонентот и логаритамот на модулот на основата на овој степен. Да го напишеме ова својство на логаритмот на моќта како формула: log a b p =p·log a |b|, каде што a>0, a≠1, b и p се броеви такви што степенот b p има смисла и b p >0.

    Прво го докажуваме ова својство за позитивно б. Основниот логаритамски идентитет ни овозможува да го претставиме бројот b како лог a b , потоа b p =(a log a b) p , а добиениот израз, поради својството на моќ, е еднаков на p·log a b . Значи, доаѓаме до еднаквоста b p =a p·log a b, од која, според дефиницијата за логаритам, заклучуваме дека log a b p =p·log a b.

    Останува да се докаже ова својство за негативно б. Овде забележуваме дека изразот log a b p за негативно b има смисла само за парни експоненти p (бидејќи вредноста на степенот b p мора да биде поголема од нула, во спротивно логаритамот нема да има смисла), а во овој случај b p =|b| стр. Тогаш b p =|b| p =(a log a |b|) p =a p·log a |b| , од каде log a b p =p·log a |b| .

    На пример, и ln(-3) 4 =4·ln|-3|=4·ln3.

    Тоа произлегува од претходниот имот својство на логаритмот од коренот: логаритамот на n-тиот корен е еднаков на производот на дропот 1/n со логаритамот на радикалниот израз, односно каде a>0, a≠1, n е природен број поголем од еден, b>0 .

    Доказот се заснова на еднаквоста (види дефиниција за експонент со фракционо експонент), која важи за секој позитивен b, и својството на логаритамот на експонентот: .

    Еве пример за користење на ова својство: .

    Сега да докажеме формула за преместување во нова логаритамска основаљубезен . За да го направите ова, доволно е да се докаже валидноста на логот за еднаквост c b=log a b·log c a. Основниот логаритамски идентитет ни овозможува да го претставиме бројот b како лог a b , потоа log c b=log c a log a b . Останува да се користи својството на логаритамот на степенот: log c a log a b =log a b·log c a . Ова ја докажува еднаквоста log c b=log a b·log c a, што значи дека е докажана и формулата за премин кон нова основа на логаритамот .

    Да покажеме неколку примери за користење на ова својство на логаритми: и .

    Формулата за преместување во нова база ви овозможува да продолжите да работите со логаритми кои имаат „погодна“ основа. На пример, може да се користи за промена на природни или децимални логаритми за да можете да ја пресметате вредноста на логаритам од табела со логаритми. Формулата за преместување во нова логаритамска основа, исто така, овозможува, во некои случаи, да се најде вредноста на даден логаритам кога се познати вредностите на некои логаритми со други основи.

    Често се користи посебен случај на формулата за премин кон нова логаритамска основа за c=b од формата. Ова покажува дека log a b и log b a се меѓусебно инверзни броеви. На пр. .

    Често се користи и формулата, што е погодно за пронаоѓање на вредностите на логаритмите. За да ги потврдиме нашите зборови, ќе покажеме како може да се користи за пресметување на вредноста на логаритам на формата. Ние имаме . За да се докаже формулата, доволно е да се користи формулата за преместување во нова основа на логаритмот a: .

    Останува да се докажат својствата на споредување на логаритмите.

    Ајде да го користиме спротивниот метод. Да претпоставиме дека за 1 >1, a 2 >1 и a 1 2 и за 0 1, log a 1 b≤log a 2 b е точно. Врз основа на својствата на логаритмите, овие неравенки може да се препишат како И соодветно, и од нив следува дека log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2, соодветно. Потоа, според својствата на моќите со по истите основимора да се задоволат еднаквостите b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2, односно a 1 ≥a 2 . Така, дојдовме до контрадикција со условот a 1 2. Ова го комплетира доказот.

    Основни својства на логаритмите

    • Материјали за лекцијата
    • Преземете ги сите формули

      • Логаритмите, како и сите броеви, можат да се собираат, одземаат и трансформираат на секој начин. Но, бидејќи логаритмите не се баш обични броеви, тука постојат правила, кои се нарекуваат главните својства.

      Дефинитивно треба да ги знаете овие правила - без нив не може да се реши ниту еден сериозен логаритамски проблем. Покрај тоа, има многу малку од нив - можете да научите сè за еден ден. Па ајде да започнеме.

      Собирање и одземање логаритми

      Размислете за два логаритма со исти основи: log a x и log a y. Потоа тие можат да се собираат и одземаат и:

      Значи, збирот на логаритми е еднаков на логаритмот на производот, а разликата е еднаква на логаритмот на количникот. Ве молиме запомнете: клучната точка овде е идентични основи. Ако причините се различни, овие правила не функционираат!

      Овие формули ќе ви помогнат да пресметате логаритамски израз дури и кога неговите поединечни делови не се разгледуваат (видете ја лекцијата „Што е логаритам“). Погледнете ги примерите и видете:

      Задача. Најдете ја вредноста на изразот: log 6 4 + log 6 9.

      Бидејќи логаритмите имаат исти основи, ја користиме формулата за збир:
      дневник 6 4 + дневник 6 9 = дневник 6 (4 9) = дневник 6 36 = 2.

      Задача. Најдете ја вредноста на изразот: log 2 48 − log 2 3.

      Основите се исти, ја користиме формулата за разлика:
      log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

      Задача. Најдете ја вредноста на изразот: log 3 135 − log 3 5.

      Повторно, основите се исти, така што имаме:
      log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

      Како што можете да видите, оригиналните изрази се составени од „лоши“ логаритми, кои не се пресметуваат одделно. Но по трансформациите се добиваат сосема нормални бројки. Многумина се изградени на овој факт тест трудови. Да, изразите слични на тестот се нудат со сета сериозност (понекогаш практично без промени) на Обединетиот државен испит.

      Извлекување на експонентот од логаритамот

      Сега да ја комплицираме задачата малку. Што ако основата или аргументот на логаритам е моќност? Тогаш експонентот на овој степен може да се извади од знакот на логаритамот според следниве правила:

    • log a x n = n · log a x ;

      • Лесно е да се види дека последното правило ги следи првите две. Но, подобро е да се запамети во секој случај - во некои случаи тоа значително ќе го намали износот на пресметките.

      Се разбира, сите овие правила имаат смисла ако се почитува ODZ на логаритмот: a > 0, a ≠ 1, x > 0. И уште една работа: научете да ги применувате сите формули не само од лево кон десно, туку и обратно , т.е. Можете да ги внесете броевите пред знакот за логаритам во самиот логаритам. Ова е она што најчесто се бара.

      Задача. Најдете ја вредноста на изразот: log 7 49 6 .

      Ајде да се ослободиме од степенот во аргументот користејќи ја првата формула:
      дневник 7 49 6 = 6 дневник 7 49 = 6 2 = 12

      Задача. Најдете го значењето на изразот:

      [Наслов за сликата]

      Забележете дека именителот содржи логаритам, чија основа и аргумент се точни моќи: 16 = 2 4 ; 49 = 7 2. Ние имаме:

      [Наслов за сликата]

      Мислам дека последниот пример бара некое појаснување. Каде отидоа логаритмите? До последен момент работиме само со именителот. Ја претставивме основата и аргументот на логаритмот што стои таму во форма на моќности и ги извадивме експонентите - добивме дропка „три ката“.

      Сега да ја погледнеме главната фракција. Броителот и именителот го содржат истиот број: log 2 7. Бидејќи log 2 7 ≠ 0, можеме да ја намалиме дропката - 2/4 ќе остане во именителот. Според правилата на аритметиката, четворката може да се пренесе на броителот, што е направено. Резултатот беше одговорот: 2.

      Транзиција кон нова основа

      Зборувајќи за правилата за собирање и одземање логаритми, конкретно нагласив дека тие работат само со исти основи. Што ако причините се различни? Што ако тие не се точни моќи со ист број?

      На помош доаѓаат формулите за транзиција кон нова основа. Да ги формулираме во форма на теорема:

      Нека е даден логаритамскиот лог a x. Тогаш за кој било број c таков што c > 0 и c ≠ 1, еднаквоста е точно:

      [Наслов за сликата]

      Конкретно, ако поставиме c = x, добиваме:

      [Наслов за сликата]

      Од втората формула произлегува дека основата и аргументот на логаритмот може да се заменат, но во овој случај целиот израз е „превртен“, т.е. логаритмот се појавува во именителот.

      Овие формули ретко се наоѓаат во обичните нумерички изрази. Можно е да се процени колку се погодни само кога се решаваат логаритамски равенки и неравенки.

      Сепак, има проблеми кои не можат да се решат воопшто освен со преселба во нова основа. Ајде да погледнеме неколку од овие:

      Задача. Најдете ја вредноста на изразот: log 5 16 log 2 25.

      Забележете дека аргументите на двата логаритма содржат точни моќи. Ајде да ги извадиме индикаторите: лог 5 16 = дневник 5 2 4 = 4лог 5 2; дневник 2 25 = дневник 2 5 2 = 2 дневник 2 5;

      Сега да го „превртиме“ вториот логаритам:

      [Наслов за сликата]

      Бидејќи производот не се менува при преуредување фактори, мирно помноживме четири и два, а потоа се занимававме со логаритми.

      Задача. Најдете ја вредноста на изразот: log 9 100 lg 3.

      Основата и аргументот на првиот логаритам се точни моќи. Ајде да го запишеме ова и да се ослободиме од индикаторите:

      [Наслов за сликата]

      Сега да се ослободиме од децимален логаритам, преместување во нова база:

      [Наслов за сликата]

      Основен логаритамски идентитет

      Често во процесот на решавање е потребно да се претстави број како логаритам на дадена основа. Во овој случај, следните формули ќе ни помогнат:

    1. n = log a a n

    2. Во првиот случај, бројот n станува експонент во аргументот. Бројот n може да биде апсолутно се, бидејќи е само логаритамска вредност.

      Втората формула е всушност парафразирана дефиниција. Така се нарекува: основен логаритамски идентитет.

      Всушност, што ќе се случи ако бројот b се подигне до таква моќ што бројот b на оваа моќност го дава бројот a? Така е: резултатот е ист број a. Прочитајте го овој пасус повторно внимателно - многу луѓе се заглавуваат на него.

      Како формули за преместување во нова основа, основниот логаритамски идентитет понекогаш е единственото можно решение.

      [Наслов за сликата]

      Забележете дека log 25 64 = log 5 8 - едноставно го зедовме квадратот од основата и аргументот на логаритамот. Земајќи ги предвид правилата за множење моќи со иста основа, добиваме:

      [Наслов за сликата]

      Ако некој не знае, ова беше вистинска задача од Единствениот државен испит :)

      Логаритамска единица и логаритамска нула

      Како заклучок, ќе дадам два идентитети кои тешко можат да се наречат својства - туку тие се последици од дефиницијата на логаритамот. Тие постојано се појавуваат во проблеми и изненадувачки им создаваат проблеми дури и на „напредните“ студенти.

      1. log a a = 1 е логаритамска единица. Запомнете еднаш засекогаш: логаритамот на која било основа a на самата основа е еднаков на еден.
      2. log a 1 = 0 е логаритамска нула. Основата a може да биде што било, но ако аргументот содржи еден, логаритамот е еднаков на нула! Бидејќи 0 = 1 е директна последица на дефиницијата.

      Тоа се сите својства. Задолжително вежбајте да ги применувате во пракса! Преземете го мамечкиот лист на почетокот на лекцијата, испечатете го и решете ги проблемите.

      Логаритам. Својства на логаритмот (собирање и одземање).

      Својства на логаритмотследи од неговата дефиниција. И така логаритамот на бројот ббазирано на Асе дефинира како експонент до кој мора да се подигне број аза да го добиете бројот б(логаритам постои само за позитивни броеви).

      Од оваа формулација произлегува дека пресметката x=log a b, е еквивалентно на решавање на равенката a x =b.На пример, дневник 2 8 = 3бидејќи 8 = 2 3 . Формулирањето на логаритмот овозможува да се оправда дека ако b=a c, потоа логаритам на бројот ббазирано на аеднакви Со. Исто така, јасно е дека темата логаритми е тесно поврзана со темата за моќи.

      Со логаритми, како и со сите броеви, можете да направите операции собирање, одземањеи да се трансформираат на секој можен начин. Но, поради фактот што логаритмите не се сосема обични броеви, овде важат нивните посебни правила, кои се нарекуваат главните својства.

      Собирање и одземање логаритми.

      Да земеме два логаритами со исти основи: логирајте xИ најавите y. Тогаш е можно да се извршат операции за собирање и одземање:

      Како што гледаме, збир на логаритмие еднаков на логаритмот на производот, и разлика логаритми- логаритам на количникот. Покрај тоа, ова е точно ако бројките А, ХИ напозитивни и a ≠ 1.

      Важно е да се напомене дека главниот аспект во овие формули се истите основи. Ако основите се различни, овие правила не важат!

      Правилата за собирање и одземање логаритми со исти основи се читаат не само од лево кон десно, туку и обратно. Како резултат на тоа, ги имаме теоремите за логаритам на производот и логаритам на количникот.

      Логаритам на производотдва позитивни броја е еднаква на збирот на нивните логаритми ; преформулирајќи ја оваа теорема го добиваме следново ако броевите А, xИ напозитивни и a ≠ 1, Тоа:

      Логаритам на количникотдва позитивни броја е еднаква на разликата помеѓу логаритмите на дивидендата и делителот. Поинаку кажано, ако бројките А, XИ напозитивни и a ≠ 1, Тоа:

      Да ги примениме горенаведените теореми за решавање примери:

      Доколку бројките xИ натогаш се негативни формула за логаритам на производотстанува бесмислено. Така, забрането е да се напише:

      бидејќи изразите log 2 (-8) и log 2 (-4) воопшто не се дефинирани (логаритамска функција на= дневник 2 Xдефинирани само за позитивни вредностиаргумент X).

      Теорема на производотприменливо не само за два, туку и за неограничен број фактори. Тоа значи дека за секој природен ки сите позитивни бројки x 1 , x 2 , . . . ,x nима идентитет:

      Од Теорема за логаритамски количникможе да се добие уште едно својство на логаритмот. Општо познато е дека дневникот а 1= 0, значи

      Ова значи дека постои еднаквост:

      Логаритми од два реципрочни бројаод истата причина ќе се разликуваат едни од други исклучиво по знак. Значи:

      Логаритам. Својства на логаритмите

      Логаритам. Својства на логаритмите

      Ајде да размислиме за еднаквоста. Дозволете ни да ги знаеме вредностите на и и сакаме да ја најдеме вредноста на.

      Односно, ние го бараме експонентот со кој треба да го затегнеме за да го добиеме.

      Нека променливата може да земе која било вистинска вредност, тогаш на променливите им се наметнуваат следните ограничувања: o" title="a>o"/> , 1″ title="a1″/>, 0″ title="b>0″ />

      Ако ги знаеме вредностите на и, а сме соочени со задача да го најдеме непознатото, тогаш за таа цел се воведува математичка операција, која се нарекува. логаритам.

      За да ја најдеме вредноста што ја земаме логаритам на бројОд страна на основа :

      Логаритмот на еден број до неговата основа е експонентот до кој мора да се подигне за да се добие .

      Тоа е основен логаритамски идентитет:

      o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

      е во суштина математичка нотација дефиниции на логаритам.

      Математичката операција на логаритам е инверзна на операцијата на степенување, така својства на логаритмисе тесно поврзани со својствата на степенот.

      Да ги наведеме главните својства на логаритми:

      (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

      d>0″/>, 1″ наслов=”d1″/>

      4.

      5.

      Следната група својства ви овозможува да го претставите експонентот на изразот под знакот на логаритам или да стои на основата на логаритамот во форма на коефициент пред знакот на логаритамот:

      6.

      7.

      8.

      9.

      Следната група формули ви овозможува да преминете од логаритам со дадена основа во логаритам со произволна основа, и се нарекува формули за преместување во нова база:

      10.

      12. (заклучок од имотот 11)

      Следниве три својства не се добро познати, но тие често се користат при решавање на логаритамски равенки или при поедноставување на изрази што содржат логаритми:

      13.

      14.

      15.

      Посебни случаи:

      — децимален логаритам

      — природен логаритам

      При поедноставување на изрази кои содржат логаритми, се користи општ пристап:

      1. Децималните дропки ги претставуваме како обични дропки.

      2. Мешани броевипретставени како неправилни дропки.

      3. Броевите во основата на логаритмот и под знакот на логаритамот ги разложуваме на едноставни фактори.

      4. Се обидуваме да ги намалиме сите логаритми на иста основа.

      5. Примени ги својствата на логаритмите.

      Ајде да погледнеме примери за поедноставување на изрази кои содржат логаритми.

      Пример 1.

      Пресметајте:

      Ајде да ги поедноставиме сите експоненти: нашата задача е да ги сведеме на логаритми, чија основа е ист број како основата на експонентот.

      ==(по својство 7)=(по својство 6) =

      Ајде да ги замениме индикаторите што ги најдовме во оригиналниот израз. Добиваме:

      Одговор: 5.25

      Пример 2. Пресметајте:

      Ајде да ги намалиме сите логаритми на основата 6 (во овој случај, логаритмите од именителот на дропката ќе „мигрираат“ до броителот):

      Ајде да ги разложиме броевите под знакот логаритам на едноставни фактори:

      Ајде да ги примениме својствата 4 и 6:

      Ајде да ја претставиме замената

      Добиваме:

      Одговор: 1

      Логаритам . Основен логаритамски идентитет.

      Својства на логаритмите. Децимален логаритам. Природен логаритам.

      Логаритам позитивен број N до основата (б > 0, б 1) е експонентот x до кој b мора да се подигне за да се добие N .

      Овој запис е еквивалентен на следново: b x = N .

      Примери: дневник 3 81 = 4, бидејќи 3 4 = 81;

      дневник 1/3 27 = – 3, бидејќи (1/3) - 3 = 3 3 = 27.

      Горенаведената дефиниција за логаритам може да се напише како идентитет:

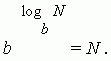
      Основни својства на логаритмите.

      2) дневник 1 = 0, бидејќи б 0 = 1 .

      3) Логаритмот на производот е еднаков на збирот на логаритмите на факторите:

      4) Логаритмот на количникот е еднаков на разликата помеѓу логаритмите на дивидендата и делителот:

      5) Логаритмот на моќта е еднаков на производот на експонентот и логаритамот на неговата основа:

      Последица на ова својство е следново: логаритам на коренот еднаков на логаритамот на радикалниот број поделен со моќноста на коренот:

      6) Ако основата на логаритмот е степен, тогаш вредноста инверзната на експонентот може да се извади од знакот за логима:

      Последните две својства може да се комбинираат во едно:

      7) Формула за преодниот модул (т.е. премин од една логаритамска основа во друга база):

      Во посебниот случај кога N=aние имаме:

      Децимален логаритам повикани основен логаритам 10. Се означува lg, т.е. дневник 10 Н= дневник Н. Логаритми на броеви 10, 100, 1000, . стр се 1, 2, 3, ..., соодветно, т.е. има толку многу позитивни

      единици, колку нули има во логаритамски број после една. Логаритми на броеви 0,1, 0,01, 0,001, . p се соодветно –1, –2, –3, …, т.е. имаат толку негативни колку што има нули во логаритамскиот број пред еден (вклучувајќи нула цели броеви). Логаритмите на другите броеви имаат фракционен дел наречен мантиса. Цел делсе нарекува логаритам карактеристика. За практична употреба, децималните логаритми се најпогодни.

      Природен логаритам повикани основен логаритам д. Се означува со ln, т.е. дневник д Н= дневник Н. Број де ирационален, неговата приближна вредност е 2,718281828. Тоа е границата кон која бројот се стреми (1 + 1 / n) nсо неограничено зголемување n(цм. првата прекрасна границана страницата „Граници“. секвенци на броеви»).
      Колку и да изгледа чудно, природните логаритми се покажаа како многу погодни при извршување на разни видови операции поврзани со анализа на функции. Пресметување логаритми до основата дсе врши многу побрзо отколку поради која било друга причина.

    • Што е потребно денес за посвојување дете во Русија? Усвојувањето во Русија, покрај одговорната лична одлука, вклучува и голем број процедури за државна верификација на кандидатите. Тешка селекција за подготвителна фазапридонесува за повеќе […]
    • Бесплатни информации за TIN или OGRN од даночниот регистар низ цела Русија - онлајн На порталот за унифицирани даночни услуги можете да добиете информации за државна регистрација правни лица, индивидуални претприемачи, […]
    • Казна за возење без документи (возачка дозвола, осигурување, СТС) Понекогаш, поради заборав, возачите седнуваат зад воланот без дозвола и добиваат казна за возење без документи. Сакаме да ве потсетиме дека автомобил ентузијаст е потребно да има […]
    • Цвеќиња за мажи. Какви цвеќиња можете да му дадете на мажот? Какви цвеќиња можете да му дадете на мажот? Нема многу „машки“ цвеќиња, но има и такви што им се даваат на мажите. Мала цветна листа пред вас: Хризантеми. Рози. Каранфили. […]
    • Меморандум за услугае посебен облик на документ кој се користи во внатрешното опкружување на едно претпријатие и служи за да брзо решениетековни проблеми со производството. Обично овој документ се составува со цел да се воведат некои […]
    • Кога и како да го добиете финансираниот дел од вашата пензија од Сбербанк? Сбербанк е партнерска банка на државниот пензиски фонд. Врз основа на ова, граѓаните кои се пријавиле за финансирана пензија може да го префрлат финансираниот дел […]
    • Детски бенефиции во Улјановск и регионот Уљановск во 2018 година Покрај тоа, програмите одобрени со федералното законодавство функционираат во сите региони. Ајде да погледнеме кој може да смета на какви придобивки. Како регионалните власти […]
    • Детален водичкако да се состави полномошно за застапување интереси индивидуалнана суд Во граѓанско или арбитражно барање, во административен или кривичен случај, интересите и на тужителот и на обвинетиот може да бидат застапувани од адвокат: […]

    Одржувањето на вашата приватност е важно за нас. Поради оваа причина, развивме Политика за приватност која опишува како ги користиме и складираме вашите информации. Ве молиме прегледајте ги нашите практики за приватност и кажете ни ако имате какви било прашања.

    Собирање и користење на лични информации

    Личните информации се однесуваат на податоци што може да се користат за идентификување или контактирање на одредена личност.

    Може да биде побарано од вас да ги дадете вашите лични податоци во секое време кога ќе не контактирате.

    Подолу се дадени неколку примери за видовите лични информации што можеме да ги собираме и како можеме да ги користиме тие информации.

    Кои лични податоци ги собираме:

    • Кога поднесувате апликација на страницата, може да собереме различни информации, вклучувајќи го вашето име, телефонски број, адреса Е-поштаитн.

    Како ги користиме вашите лични податоци:

    • Собрани од нас лични податоцини овозможува да ве контактираме и да ве информираме за уникатни понуди, промоции и други настани и претстојни настани.
    • Од време на време, може да ги користиме вашите лични податоци за да испраќаме важни известувања и комуникации.
    • Може да користиме и лични информации за внатрешни цели, како што се спроведување ревизии, анализа на податоци и разни истражувања со цел да ги подобриме услугите што ги обезбедуваме и да ви дадеме препораки во врска со нашите услуги.
    • Доколку учествувате во наградно извлекување, натпревар или слична промоција, ние може да ги користиме информациите што ги давате за администрирање на такви програми.

    Откривање информации на трети страни

    Ние не ги откриваме информациите добиени од вас на трети страни.

    Исклучоци:

    • Доколку е потребно, во согласност со закон, судска постапка, во правни постапки и/или врз основа на јавни прашања или барања од владини агенциина територијата на Руската Федерација - обелоденете ги вашите лични податоци. Ние, исто така, може да откриеме информации за вас ако утврдиме дека таквото откривање е неопходно или соодветно за безбедност, спроведување на законот или други цели од јавна важност.
    • Во случај на реорганизација, спојување или продажба, можеме да ги пренесеме личните информации што ги собираме на соодветната трета страна наследник.

    Заштита на лични информации

    Преземаме мерки на претпазливост - вклучувајќи административни, технички и физички - за да ги заштитиме вашите лични информации од губење, кражба и злоупотреба, како и од неовластен пристап, откривање, менување и уништување.

    Почитување на вашата приватност на ниво на компанија

    За да се осигураме дека вашите лични информации се безбедни, ние ги пренесуваме стандардите за приватност и безбедност на нашите вработени и строго ги спроведуваме практиките за приватност.

    Следи од неговата дефиниција. И така логаритамот на бројот ббазирано на Асе дефинира како експонент до кој мора да се подигне број аза да го добиете бројот б(логаритам постои само за позитивни броеви).

    Од оваа формулација произлегува дека пресметката x=log a b, е еквивалентно на решавање на равенката a x =b.На пример, дневник 2 8 = 3бидејќи 8 = 2 3 . Формулирањето на логаритмот овозможува да се оправда дека ако b=a c, потоа логаритам на бројот ббазирано на аеднакви Со. Исто така, јасно е дека темата за логаритми е тесно поврзана со темата за силите на бројот.

    Со логаритми, како и со сите броеви, можете да направите операции собирање, одземањеи да се трансформираат на секој можен начин. Но, поради фактот што логаритмите не се сосема обични броеви, овде важат нивните посебни правила, кои се нарекуваат главните својства.

    Собирање и одземање логаритми.

    Да земеме два логаритами со исти основи: логирајте xИ најавите y. Тогаш е можно да се извршат операции за собирање и одземање:

    log a x+ log a y= log a (x·y);

    log a x - log a y = log a (x:y).

    дневник а(x 1 . x 2 . x 3 ... x k) = логирајте x 1 + логирајте x 2 + логирајте x 3 + ... + log a x k.

    Од Теорема за логаритамски количникможе да се добие уште едно својство на логаритмот. Општо познато е дека дневникот а 1= 0, значи

    дневник а 1 /б= дневник а 1 - дневник а б= -лог а б.

    Ова значи дека постои еднаквост:

    log a 1 / b = - log a b.

    Логаритми од два реципрочни бројаод истата причина ќе се разликуваат едни од други исклучиво по знак. Значи:

    Дневник 3 9= - дневник 3 1 / 9 ; дневник 5 1 / 125 = - дневник 5 125.

    Со ова видео започнувам долга серија лекции за логаритамските равенки. Сега имате три примери пред вас, врз основа на кои ќе научиме да решаваме најмногу едноставни задачи, кои се нарекуваат т.н. протозои.

    log 0,5 (3x − 1) = −3

    дневник (x + 3) = 3 + 2 дневник 5

    Дозволете ми да ве потсетам дека наједноставната логаритамска равенка е следнава:

    log a f(x) = b

    Во овој случај, важно е променливата x да е присутна само внатре во аргументот, односно само во функцијата f (x). И броевите a и b се само броеви и во никој случај не се функции што ја содржат променливата x.

    Основни методи на решение

    Постојат многу начини за решавање на такви структури. На пример, повеќето наставници во училиштето го нудат овој метод: Веднаш изразете ја функцијата f (x) користејќи ја формулата f ( x) = а б . Односно, кога ќе наидете на наједноставната конструкција, можете веднаш да преминете на решението без дополнителни дејства и конструкции.

    Да, се разбира, одлуката ќе биде точна. Меѓутоа, проблемот со оваа формула е што повеќето студенти не разбираат, од каде доаѓа и зошто буквата а ја подигаме на буквата б.

    Како резултат на тоа, често гледам многу досадни грешки кога, на пример, овие букви се заменуваат. Оваа формула мора или да се разбере или да се преполни, а вториот метод води до грешки во најнеповолните и најклучните моменти: за време на испити, тестови итн.

    Затоа им предлагам на сите мои ученици да ја напуштат стандардната училишна формула и да го користат вториот пристап за решавање логаритамски равенки, кој, како што веројатно претпоставувате од името, се нарекува канонска форма.

    Идејата за канонската форма е едноставна. Ајде повторно да го разгледаме нашиот проблем: лево имаме лог a, а под буквата a мислиме број, а во никој случај функција која ја содржи променливата x. Следствено, ова писмо подлежи на сите ограничувања што се наметнуваат врз основа на логаритамот. имено:

    1 ≠ a > 0

    Од друга страна, од истата равенка гледаме дека логаритамот мора да биде еднаков на бројот b, а на оваа буква не се наметнуваат никакви ограничувања, бидејќи може да земе каква било вредност - и позитивна и негативна. Сè зависи од тоа кои вредности ги зема функцијата f(x).

    И тука се сеќаваме на нашето прекрасно правило дека кој било број b може да се претстави како логаритам на основата a на a до моќта на b:

    b = log a a b

    Како да се запамети оваа формула? Да, многу едноставно. Ајде да ја напишеме следната конструкција:

    b = b 1 = b log a a

    Се разбира, во овој случај произлегуваат сите ограничувања што ги запишавме на почетокот. Сега да го искористиме основното својство на логаритамот и да го воведеме множителот b како моќност на a. Добиваме:

    b = b 1 = b log a a = log a a b

    Како резултат на тоа, оригиналната равенка ќе биде препишана на следниов начин:

    log a f (x) = log a a b → f (x) = a b

    Тоа е се. Новата функција повеќе не содржи логаритам и може да се реши со помош на стандардни алгебарски техники.

    Се разбира, некој сега ќе се спротивстави: зошто воопшто беше неопходно да се дојде до некаква канонска формула, зошто да се извршат два дополнителни непотребни чекори ако беше можно веднаш да се пресели од оригиналниот дизајн до конечната формула? Да, само затоа што повеќето студенти не разбираат од каде доаѓа оваа формула и, како резултат на тоа, редовно прават грешки при примената.

    Но, оваа низа на дејства, која се состои од три чекори, ви овозможува да ја решите оригиналната логаритамска равенка, дури и ако не разбирате од каде доаѓа конечната формула. Патем, овој запис се нарекува канонска формула:

    log a f (x) = log a a b

    Практичноста на канонската форма лежи и во фактот што може да се користи за решавање на многу широка класа на логаритамски равенки, а не само за наједноставните што ги разгледуваме денес.

    Примери на решенија

    Сега ајде да погледнеме вистински примери. Значи, да одлучиме:

    log 0,5 (3x − 1) = −3

    Ајде да го преработиме вака:

    log 0,5 (3x − 1) = log 0,5 0,5 −3

    Многу студенти брзаат и се обидуваат веднаш да го подигнат бројот 0,5 на моќта што ни дојде од првичниот проблем. Навистина, кога веќе сте добро обучени за решавање на вакви проблеми, можете веднаш да го извршите овој чекор.

    Меѓутоа, ако сега само што почнувате да ја проучувате оваа тема, подобро е да не брзате никаде за да избегнете правење навредливи грешки. Значи, ја имаме канонската форма. Ние имаме:

    3x − 1 = 0,5 −3

    Ова повеќе не е логаритамска равенка, туку линеарна во однос на променливата x. За да го решиме, прво да го погледнеме бројот 0,5 со моќност од −3. Забележете дека 0,5 е 1/2.

    (1/2) −3 = (2/1) 3 = 8

    Претворете ги сите децимални дропки во обични дропки кога решавате логаритамска равенка.

    Ние препишуваме и добиваме:

    3x − 1 = 8
    3x = 9
    x = 3

    Тоа е тоа, го добивме одговорот. Првиот проблем е решен.

    Втора задача

    Ајде да преминеме на втората задача:

    Како што гледаме, оваа равенка повеќе не е наједноставна. Ако само затоа што има разлика лево, а ниту еден логаритам до една основа.

    Затоа, треба некако да се ослободиме од оваа разлика. ВО во овој случајсè е многу едноставно. Да ги погледнеме подетално основите: лево е бројот под коренот:

    Општа препорака: во сите логаритамски равенки, обидете се да се ослободите од радикалите, т.е., од записите со корени и преминете на моќ функции, едноставно затоа што експонентите на овие моќи лесно се вадат од знакот на логаритмот и, во крајна линија, таквата нотација значително ги поедноставува и забрзува пресметките. Ајде да го запишеме вака:

    Сега да се потсетиме на извонредното својство на логаритмот: моќите може да се изведат од аргументот, како и од основата. Во случај на основа, се случува следново:

    log a k b = 1/k лога b

    Со други зборови, бројот што бил во основната моќност се носи напред и во исто време се превртува, односно станува реципрочен број. Во нашиот случај, основниот степен беше 1/2. Затоа, можеме да го извадиме како 2/1. Добиваме:

    5 2 log 5 x − log 5 x = 18
    10 log 5 x − log 5 x = 18

    Ве молиме запомнете: во никој случај не треба да се ослободите од логаритмите на овој чекор. Запомнете математика од 4-5 одделение и редоследот на операциите: прво се врши множење, а дури потоа собирање и одземање. Во овој случај, одземаме еден од истите елементи од 10 елементи:

    9 дневник 5 x = 18
    дневник 5 x = 2

    Сега нашата равенка изгледа како што треба. Ова наједноставен дизајн, и го решаваме користејќи ја канонската форма:

    дневник 5 x = дневник 5 5 2
    x = 5 2
    x = 25

    Тоа е се. Вториот проблем е решен.

    Трет пример

    Да преминеме на третата задача:

    дневник (x + 3) = 3 + 2 дневник 5

    Дозволете ми да ве потсетам на следнава формула:

    лог б = дневник 10 б

    Ако поради некоја причина сте збунети од дневникот за нотација b, тогаш кога ги извршувате сите пресметки можете едноставно да напишете дневник 10 b. Можете да работите со децимални логаритми на ист начин како и со другите: земете моќи, собирајте и претставувајте ги сите броеви во форма lg 10.

    Токму овие својства сега ќе ги користиме за да го решиме проблемот, бидејќи не е наједноставниот што го запишавме на самиот почеток на нашата лекција.

    Прво, забележете дека факторот 2 пред lg 5 може да се додаде и да стане моќност на основата 5. Покрај тоа, слободниот член 3 може да се претстави и како логаритам - ова е многу лесно да се набљудува од нашата нотација.

    Проценете сами: кој било број може да се претстави како дневник до основата 10:

    3 = дневник 10 10 3 = дневник 10 3

    Ајде да го преработиме оригиналниот проблем земајќи ги предвид добиените промени:

    лог (x − 3) = лог 1000 + лог 25
    лог (x − 3) = лог 1000 25
    лог (x − 3) = лог 25.000

    Пред нас повторно е канонската форма, а ние ја добивме без да поминеме низ фазата на трансформација, односно никаде не се појави наједноставната логаритамска равенка.

    Токму за ова зборував на самиот почеток на лекцијата. Канонската форма ви овозможува да решите поширока класа на проблеми од стандардната училишна формула дадена од повеќето училишни наставници.

    Па, тоа е сè, се ослободуваме од знакот на децималниот логаритам и добиваме едноставна линеарна конструкција:

    x + 3 = 25.000
    x = 24.997

    Сите! Проблемот е решен.

    Забелешка за опсегот

    Овде би сакал да направам важна забелешка во однос на опсегот на дефиницијата. Сега сигурно ќе има ученици и наставници кои ќе речат: „Кога ги решаваме изразите со логаритми, мора да запомниме дека аргументот f (x) мора да биде поголем од нула!“ Во овој поглед, се поставува логично прашање: зошто не баравме оваа нееднаквост да биде задоволена во ниту еден од разгледаните проблеми?

    Не се грижи. Во овие случаи, нема да се појават дополнителни корени. И ова е уште еден одличен трик кој ви овозможува да го забрзате решението. Само знајте дека ако во проблемот променливата x се појавува само на едно место (или подобро, во еден аргумент на еден логаритам), и никаде на друго место во нашиот случај не се појавува променливата x, тогаш запишете го доменот на дефиниција нема потреба, бидејќи ќе се изврши автоматски.

    Проценете сами: во првата равенка добивме дека 3x − 1, т.е. аргументот треба да биде еднаков на 8. Ова автоматски значи дека 3x − 1 ќе биде поголемо од нула.

    Со истиот успех можеме да напишеме дека во вториот случај x треба да биде еднакво на 5 2, односно сигурно е поголемо од нула. И во третиот случај, каде што x + 3 = 25.000, т.е., повторно, очигледно поголемо од нула. Со други зборови, опсегот се задоволува автоматски, но само ако x се појавува само во аргументот на само еден логаритам.

    Тоа е се што треба да знаете за да ги решите наједноставните проблеми. Само ова правило, заедно со правилата за трансформација, ќе ви овозможи да решите многу широка класа на проблеми.

    Но, да бидеме искрени: за конечно да ја разбереме оваа техника, со цел да научиме како да ја користиме канонската форма логаритамска равенка, не е доволно само да гледате една видео лекција. Затоа преземете ги опциите токму сега за независна одлука, кои се прикачени на оваа видео лекција и започнуваат да решаваат барем една од овие две самостојни дела.

    Ќе ви одземе буквално неколку минути. Но, ефектот од таквата обука ќе биде многу поголем отколку ако едноставно ја гледавте оваа видео лекција.

    Се надевам дека оваа лекција ќе ви помогне да ги разберете логаритамските равенки. Користете ја канонската форма, поедноставете ги изразите користејќи ги правилата за работа со логаритми - и нема да се плашите од никакви проблеми. Тоа е се што имам за денес.

    Земајќи го предвид доменот на дефиниција

    Сега да зборуваме за доменот на дефинирање на логаритамската функција и како тоа влијае на решавањето на логаритамските равенки. Размислете за конструкција на формата

    log a f(x) = b

    Таквиот израз се нарекува наједноставен - содржи само една функција, а броевите a и b се само броеви и во никој случај функција која зависи од променливата x. Тоа може да се реши многу едноставно. Вие само треба да ја користите формулата:

    b = log a a b

    Оваа формула е едно од клучните својства на логаритмот, а при замена во нашиот оригинален израз го добиваме следново:

    log a f (x) = log a a b

    f (x) = a b

    Ова е позната формула од училишните учебници. Многу студенти веројатно ќе имаат прашање: бидејќи во оригиналниот израз функцијата f (x) е под знакот за дневник, на неа се наметнуваат следните ограничувања:

    f(x) > 0

    Ова ограничување се применува бидејќи логаритмот на негативни броевине постои. Значи, можеби, како резултат на ова ограничување, треба да се воведе проверка на одговорите? Можеби тие треба да се вметнат во изворот?

    Не, во наједноставните логаритамски равенки дополнителна проверка е непотребна. И затоа. Погледнете ја нашата конечна формула:

    f (x) = a b

    Факт е дека бројот a е во секој случај поголем од 0 - ова барање го наметнува и логаритамот. Бројот а е основа. Во овој случај, не се наметнуваат ограничувања за бројот б. Но, ова не е важно, бидејќи без разлика кој степен го подигаме позитивен број, сепак ќе добиеме позитивен број на излезот. Така, барањето f (x) > 0 се задоволува автоматски.

    Она што навистина вреди да се провери е доменот на функцијата под знакот за дневник. Може да има доста комплексни дизајни, а при процесот на одлучување тие мора да бидат следени. Ајде да погледнеме.

    Прва задача:

    Прв чекор: претворете ја дропот десно. Добиваме:

    Се ослободуваме од знакот логаритам и ја добиваме вообичаената ирационална равенка:

    Од добиените корени ни одговара само првиот, бидејќи вториот корен помалку од нула. Единствениот одговор ќе биде бројот 9. Тоа е тоа, проблемот е решен. Никој дополнителни проверкифактот дека изразот под знакот логаритам е поголем од 0 не е потребен, бидејќи тој не е само поголем од 0, туку според условот на равенката е еднаков на 2. Затоа, барањето „поголемо од нула“ е задоволен автоматски.

    Ајде да преминеме на втората задача:

    Сè е исто овде. Ја препишуваме конструкцијата, заменувајќи ја тројната:

    Се ослободуваме од логаритамските знаци и добиваме ирационална равенка:

    Ги квадратуваме двете страни земајќи ги предвид ограничувањата и добиваме:

    4 − 6x − x 2 = (x − 4) 2

    4 − 6x − x 2 = x 2 + 8x + 16

    x 2 + 8x + 16 −4 + ​​6x + x 2 = 0

    2x 2 + 14x + 12 = 0 |:2

    x 2 + 7x + 6 = 0

    Добиената равенка ја решаваме преку дискриминантата:

    D = 49 − 24 = 25

    x 1 = −1

    x 2 = −6

    Но, x = −6 не ни одговара, бидејќи ако го замениме овој број во нашата неравенка, добиваме:

    −6 + 4 = −2 < 0

    Во нашиот случај, потребно е да биде поголемо од 0 или, во екстремни случаи, еднакво. Но, x = −1 ни одговара:

    −1 + 4 = 3 > 0

    Единствениот одговор во нашиот случај ќе биде x = −1. Тоа е решението. Да се ​​вратиме на самиот почеток на нашите пресметки.

    Главната работа од оваа лекција е дека не треба да ги проверувате ограничувањата на функцијата во едноставни логаритамски равенки. Бидејќи во текот на процесот на решавање сите ограничувања се задоволуваат автоматски.

    Сепак, ова во никој случај не значи дека можете целосно да заборавите на проверката. Во процесот на работа на логаритамска равенка, таа може добро да се претвори во ирационална, која ќе има свои ограничувања и барања за десната страна, што ги видовме денес во два различни примери.

    Слободно решавајте ги ваквите проблеми и бидете особено внимателни доколку има корен во расправијата.

    Логаритамски равенки со различни основи

    Продолжуваме да ги проучуваме логаритамските равенки и целосно ќе анализираме уште две интересен прием, со чија помош е модерно да се реши повеќе комплексни дизајни. Но, прво, да се потсетиме како се решаваат наједноставните проблеми:

    log a f(x) = b

    Во овој запис a и b се броеви, а во функцијата f (x) променливата x мора да биде присутна и само таму, односно x мора да биде само во аргументот. Ваквите логаритамски равенки ќе ги трансформираме користејќи ја канонската форма. За да го направите ова, забележете дека

    b = log a a b

    Покрај тоа, a b е токму аргумент. Ајде да го преработиме овој израз на следниов начин:

    log a f (x) = log a a b

    Токму тоа се обидуваме да го постигнеме, за да има логаритам за да се заснова a и на левата и на десната страна. Во овој случај, можеме, фигуративно кажано, да ги пречкртаме знаците на дневникот и од математичка гледна точка можеме да кажеме дека едноставно ги изедначуваме аргументите:

    f (x) = a b

    Како резултат на тоа, ќе добиеме нов израз кој ќе биде многу полесен за решавање. Ајде да го примениме ова правило за нашите проблеми денес.

    Значи, првиот дизајн:

    Најпрво, забележувам дека десно е дропка чиј именител е лог. Кога ќе видите ваков израз, добро е да се сетите на едно прекрасно својство на логаритмите:

    Преведено на руски, тоа значи дека секој логаритам може да се претстави како количник на два логаритами со која било основа c. Секако 0< с ≠ 1.

    Значи: оваа формула има еден прекрасен посебен случај, кога променливата c е еднаква на променливата б. Во овој случај добиваме конструкција како:

    Токму оваа конструкција ја гледаме од знакот десно во нашата равенка. Да ја замениме оваа конструкција со log a b , добиваме:

    Со други зборови, во споредба со првичната задача, ги заменивме аргументите и основата на логаритмот. Наместо тоа, моравме да ја смениме дропот.

    Да запомниме дека кој било степен може да се изведе од основата според следново правило:

    Со други зборови, коефициентот k, кој е моќност на основата, се изразува како превртена дропка. Да го претставиме како превртена дропка:

    Дробниот фактор не може да се остави напред, бидејќи во овој случај нема да можеме да ја претставиме оваа нотација како канонска форма (на крајот на краиштата, во канонската форма нема дополнителен фактор пред вториот логаритам). Затоа, да ја додадеме дропот 1/4 на аргументот како моќност:

    Сега ги изедначуваме аргументите чии основи се исти (а нашите основи се навистина исти) и пишуваме:

    x + 5 = 1

    x = −4

    Тоа е се. Го добивме одговорот на првата логаритамска равенка. Ве молиме имајте предвид: во оригиналниот проблем, променливата x се појавува само во еден дневник и се појавува во нејзиниот аргумент. Затоа, нема потреба да се провери доменот, а нашиот број x = −4 е навистина одговорот.

    Сега да преминеме на вториот израз:

    log 56 = log 2 log 2 7 − 3log (x + 4)

    Овде, покрај вообичаените логаритми, ќе треба да работиме и со log f (x). Како да се реши таква равенка? На неподготвен ученик може да му се чини дека ова е некаква тешка задача, но всушност сè може да се реши на елементарен начин.

    Погледнете внимателно на терминот lg 2 log 2 7. Што можеме да кажеме за него? Основите и аргументите на log и lg се исти, и ова треба да даде некои идеи. Да се ​​потсетиме уште еднаш како се вадат моќите под знакот на логаритамот:

    log a b n = nlog a b

    Со други зборови, она што беше моќ на b во аргументот станува фактор пред самиот лог. Да ја примениме оваа формула за изразот lg 2 log 2 7. Не плашете се од lg 2 - ова е најчестиот израз. Можете да го преработите на следниов начин:

    За него важат сите правила кои важат за кој било друг логаритам. Конкретно, факторот напред може да се додаде на степенот на аргументот. Ајде да го запишеме:

    Многу често, учениците не ја гледаат оваа акција директно, бидејќи не е добро да се внесе еден дневник под знакот на друг. Всушност, нема ништо криминално во ова. Покрај тоа, добиваме формула што е лесно да се пресмета ако се сеќавате на важно правило:

    Оваа формула може да се смета и како дефиниција и како едно од нејзините својства. Во секој случај, ако конвертирате логаритамска равенка, треба да ја знаете оваа формула исто како што би ја знаеле логирачката претстава на кој било број.

    Да се ​​вратиме на нашата задача. Го препишуваме земајќи го предвид фактот дека првиот член десно од знакот за еднакво ќе биде едноставно еднаков на lg 7. Имаме:

    lg 56 = lg 7 − 3lg (x + 4)

    Да го преместиме lg 7 налево, добиваме:

    lg 56 − log 7 = −3lg (x + 4)

    Ги одземаме изразите лево затоа што имаат иста основа:

    lg (56/7) = -3lg (x + 4)

    Сега да ја разгледаме подетално равенката што ја добивме. Тоа е практично канонската форма, но има фактор −3 на десната страна. Ајде да го додадеме во вистинскиот аргумент на lg:

    лог 8 = лог (x + 4) −3

    Пред нас е канонската форма на логаритамската равенка, па ги пречкртаме знаците lg и ги изедначуваме аргументите:

    (x + 4) −3 = 8

    x + 4 = 0,5

    Тоа е се! Ја решивме втората логаритамска равенка. Во овој случај, не се потребни дополнителни проверки, бидејќи во оригиналниот проблем x беше присутен само во еден аргумент.

    Пак ќе го наведам клучните точкиоваа лекција.

    Главната формула што се учи во сите лекции на оваа страница посветена на решавање на логаритамски равенки е канонската форма. И не плашете се од фактот дека повеќето училишни учебници ве учат да ги решавате ваквите проблеми поинаку. Оваа алатка работи многу ефикасно и ви овозможува да решите многу поширока класа на проблеми од наједноставните што ги проучувавме на самиот почеток на нашата лекција.

    Покрај тоа, за решавање на логаритамски равенки ќе биде корисно да се знаат основните својства. Имено:

    1. Формулата за преместување во една база и специјалниот случај кога го реверзираме дневникот (ова ни беше многу корисно во првиот проблем);
    2. Формула за собирање и одземање моќи од знакот логаритам. Овде, многу студенти заглавуваат и не гледаат дека извадената и воведена диплома може сама по себе да содржи лог f (x). Ништо лошо во тоа. Можеме да воведеме еден дневник според знакот на другиот и во исто време значително да го поедноставиме решението на проблемот, што е она што го забележуваме во вториот случај.

    Како заклучок, би сакал да додадам дека не е неопходно да се провери доменот на дефиниција во секој од овие случаи, бидејќи секаде променливата x е присутна само во еден знак на лог, а во исто време е и во нејзиниот аргумент. Како последица на тоа, сите барања од опсегот се исполнуваат автоматски.

    Проблеми со променлива основа

    Денес ќе ги разгледаме логаритамските равенки, кои за многу студенти изгледаат нестандардни, ако не и целосно нерешливи. Зборуваме за изрази кои не се засноваат на бројки, туку на променливи, па дури и функции. Ваквите конструкции ќе ги решаваме користејќи ја нашата стандардна техника, имено преку канонската форма.

    Прво, да се потсетиме како се решаваат наједноставните проблеми, врз основа на обични броеви. Значи, наједноставната конструкција се нарекува

    log a f(x) = b

    За да ги решиме ваквите проблеми, можеме да ја користиме следната формула:

    b = log a a b

    Го препишуваме нашиот оригинален израз и добиваме:

    log a f (x) = log a a b

    Потоа ги изедначуваме аргументите, т.е. пишуваме:

    f (x) = a b

    Така, се ослободуваме од знакот за дневник и го решаваме вообичаениот проблем. Во овој случај, корените добиени од решението ќе бидат корените на првобитната логаритамска равенка. Дополнително, записот кога и левата и десната страна се во ист логаритам со иста основа, прецизно се нарекува канонска форма. До таков рекорд ќе се обидеме да ги намалиме денешните дизајни. Значи, да одиме.

    Прва задача:

    лог x − 2 (2x 2 − 13x + 18) = 1

    Заменете го 1 со лог x − 2 (x − 2) 1 . Степенот што го набљудуваме во аргументот е всушност бројот b што стои десно од знакот за еднаквост. Така, да го преработиме нашиот израз. Добиваме:

    log x − 2 (2x 2 − 13x + 18) = log x − 2 (x − 2)

    Што гледаме? Пред нас е канонската форма на логаритамската равенка, така што можеме безбедно да ги изедначуваме аргументите. Добиваме:

    2x 2 − 13x + 18 = x − 2

    Но, решението не завршува тука, бидејќи дадена равенкане е еквивалентно на оригиналот. На крајот на краиштата, добиената конструкција се состои од функции што се дефинирани на целата бројна линија, а нашите оригинални логаритми не се дефинирани насекаде и не секогаш.

    Затоа, мора посебно да го запишеме доменот на дефиниција. Да не се делиме влакна и прво да ги запишеме сите барања:

    Прво, аргументот на секој од логаритмите мора да биде поголем од 0:

    2x 2 − 13x + 18 > 0

    x − 2 > 0

    Второ, основата не само што треба да биде поголема од 0, туку и да се разликува од 1:

    x − 2 ≠ 1

    Како резултат, го добиваме системот:

    Но, не плашете се: кога се обработуваат логаритамски равенки, таков систем може значително да се поедностави.

    Проценете сами: од една страна, од нас се бара квадратната функција да биде поголема од нула, а од друга страна, оваа квадратна функција е изедначена со одреден линеарен израз, кој исто така се бара да биде поголем од нула.

    Во овој случај, ако бараме дека x − 2 > 0, тогаш барањето 2x 2 − 13x + 18 > 0 автоматски ќе биде задоволено квадратна функција. Така, бројот на изрази содржани во нашиот систем ќе се намали на три.

    Се разбира, исто толку добро би можеле да пречкртаме линеарна нееднаквост, односно, прецртајте x − 2 > 0 и барајте 2x 2 − 13x + 18 > 0. Но, мора да се согласите дека решавањето на наједноставната линеарна неравенка е многу побрзо и полесно од квадратното, дури и ако е резултат на решавање на целата овој систем ќе ги добиеме истите корени.

    Во принцип, обидете се да ги оптимизирате пресметките секогаш кога е можно. И во случај на логаритамски равенки, пречкртајте ги најтешките неравенки.

    Ајде да го преработиме нашиот систем:

    Еве еден систем од три изрази, од кои два, всушност, веќе се занимававме. Ајде да го запишеме одделно квадратна равенкаи ајде да го решиме:

    2x 2 − 14x + 20 = 0

    x 2 − 7x + 10 = 0

    Пред нас е намален квадратен трином и, според тоа, можеме да ги користиме формулите на Виета. Добиваме:

    (x − 5) (x − 2) = 0

    x 1 = 5

    x 2 = 2

    Сега се враќаме на нашиот систем и откриваме дека x = 2 не ни одговара, бидејќи од нас се бара x да биде строго поголем од 2.

    Но, x = 5 ни одговара совршено: бројот 5 е поголем од 2, а во исто време 5 не е еднаков на 3. Затоа, единственото решение за овој систем ќе биде x = 5.

    Тоа е тоа, проблемот е решен, вклучително и земајќи го предвид ОДЗ. Да преминеме на втората равенка. Повеќе интересни и информативни пресметки не очекуваат овде:

    Првиот чекор: како и минатиот пат, целата оваа работа ја доведуваме во канонска форма. За да го направите ова, можеме да го напишеме бројот 9 на следниов начин:

    Не мора да ја допирате основата со коренот, но подобро е да го трансформирате аргументот. Ајде да одиме од корен до моќ в рационален индикатор. Ајде да запишеме:

    Да не ја препишувам целата наша голема логаритамска равенка, туку веднаш да ги изедначам аргументите:

    x 3 + 10x 2 + 31x + 30 = x 3 + 9x 2 + 27x + 27

    x 2 + 4x + 3 = 0

    Пред нас е ново намален квадратен трином, да ги искористиме формулите на Виета и да напишеме:

    (x + 3) (x + 1) = 0

    x 1 = −3

    x 2 = −1

    Значи, ги добивме корените, но никој не ни гарантира дека ќе одговараат на првобитната логаритамска равенка. На крајот на краиштата, знаците за дневници наметнуваат дополнителни ограничувања (тука требаше да го запишеме системот, но поради гломазната природа на целата структура, решив да го пресметам доменот на дефиниција одделно).

    Пред сè, запомнете дека аргументите мора да бидат поголеми од 0, имено:

    Тоа се барањата наметнати од опсегот на дефиницијата.

    Веднаш да забележиме дека со оглед на тоа што ги поистоветуваме првите два изрази на системот еден со друг, можеме да прецртаме кој било од нив. Ајде да го пречкртаме првиот бидејќи изгледа позаканувачки од вториот.

    Дополнително, забележете дека решението за втората и третата неравенка ќе бидат истите множества (коцката на некој број е поголема од нула, ако самиот тој број е поголем од нула; слично, со корен од третиот степен - овие неравенки се целосно аналогни, па можеме да го пречкртаме).

    Но, со третата нееднаквост ова нема да функционира. Ајде да се ослободиме од радикалниот знак лево со подигање на двата дела на коцка. Добиваме:

    Значи, ги добиваме следниве барања:

    − 2 ≠ x > −3

    Кој од нашите корени: x 1 = −3 или x 2 = −1 ги исполнува овие барања? Очигледно, само x = −1, бидејќи x = −3 не ја задоволува првата неравенка (бидејќи нашата неравенка е строга). Значи, враќајќи се на нашиот проблем, добиваме еден корен: x = −1. Тоа е тоа, проблемот е решен.

    Уште еднаш, клучните точки на оваа задача:

    1. Слободно применувајте и решавајте логаритамски равенки користејќи канонска форма. Учениците кои пишуваат на овој начин, наместо да одат директно од оригиналниот проблем на конструкција како log a f (x) = b, дозволуваат многу помалку грешкиод оние кои брзаат некаде, прескокнувајќи средни чекори на пресметки;
    2. Штом променлива основа се појави во логаритам, проблемот престанува да биде наједноставен. Затоа, при неговото решавање, потребно е да се земе предвид доменот на дефиниција: аргументите мора да бидат поголеми од нула, а основите не само што треба да бидат поголеми од 0, туку не смеат да бидат и еднакви на 1.

    Конечните барања може да се применат на конечните одговори на различни начини. На пример, можете да решите цел систем кој ги содржи сите барања за доменот на дефиниција. Од друга страна, прво можете да го решите самиот проблем, а потоа да го запомните доменот на дефиниција, одделно да го разработите во форма на систем и да го примените на добиените корени.

    Кој метод да го изберете при решавање на одредена логаритамска равенка зависи од вас. Во секој случај, одговорот ќе биде ист.

    \(a^(b)=c\) \(\лева десна стрелка\) \(\log_(a)(c)=b\)

    Да објасниме поедноставно. На пример, \(\log_(2)(8)\) е еднакво на моќноста на која \(2\) мора да се подигне за да се добие \(8\). Од ова е јасно дека \(\log_(2)(8)=3\).

    Примери:

    \(\log_(5)(25)=2\)

    бидејќи \(5^(2)=25\)

    \(\log_(3)(81)=4\)

    бидејќи \(3^(4)=81\)

    \(\log_(2)\)\(\frac(1)(32)\) \(=-5\)

    бидејќи \(2^(-5)=\)\(\frac(1)(32)\)

    Аргумент и основа на логаритам

    Секој логаритам ја има следната „анатомија“:

    Аргументот на логаритам обично се пишува на негово ниво, а основата е напишана во знак поблиску до знакот логаритам. И овој запис гласи вака: „логаритам од дваесет и пет до основата пет“.

    Како да се пресмета логаритам?

    За да го пресметате логаритамот, треба да одговорите на прашањето: до која сила треба да се подигне основата за да се добие аргументот?

    На пример, пресметај го логаритамот: а) \(\log_(4)(16)\) б) \(\log_(3)\)\(\frac(1)(3)\) в) \(\log_(\ sqrt (5))(1)\) г) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

    а) До која сила треба да се подигне \(4\) за да се добие \(16\)? Очигледно вториот. Затоа:

    \(\log_(4)(16)=2\)

    \(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

    в) До која моќ треба да се подигне \(\sqrt(5)\) за да се добие \(1\)? Која моќ го прави секој број еден? Нула, се разбира!

    \(\log_(\sqrt(5))(1)=0\)

    г) До која сила треба да се подигне \(\sqrt(7)\) за да се добие \(\sqrt(7)\)? Прво, секој број до првата сила е еднаков на самиот себе.

    \(\log_(\sqrt(7))(\sqrt(7))=1\)

    д) До која моќност мора да се подигне \(3\) за да се добие \(\sqrt(3)\)? Од знаеме што е тоа фракциона моќност, а тоа значи Квадратен корене моќта на \(\frac(1)(2)\) .

    \(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

    Пример : Пресметај логаритам \(\log_(4\sqrt(2))(8)\)

    Решение :

    \(\log_(4\sqrt(2))(8)=x\)

    Треба да ја најдеме вредноста на логаритамот, да ја означиме како x. Сега да ја користиме дефиницијата за логаритам:
    \(\log_(a)(c)=b\) \(\лева стрелка\) \(a^(b)=c\)

    \((4\sqrt(2))^(x)=8\)

    Што ги поврзува \(4\sqrt(2)\) и \(8\)? Два, бидејќи и двата броја може да се претстават со два:
    \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)

    \(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)

    Лево ги користиме својствата на степенот: \(a^(m)\cdot a^(n)=a^(m+n)\) и \((a^(m))^(n)= a^(m\cточка n)\)

    \(2^(\frac(5)(2)x)=2^(3)\)

    Основите се еднакви, преминуваме на еднаквост на индикаторите

    \(\frac(5x)(2)\) \(=3\)

    Помножете ги двете страни на равенката со \(\frac(2)(5)\)

    Резултирачкиот корен е вредноста на логаритмот

    Одговори : \(\log_(4\sqrt(2))(8)=1,2\)

    Зошто е измислен логаритамот?

    За да го разбереме ова, да ја решиме равенката: \(3^(x)=9\). Само поклопете го \(x\) за равенката да функционира. Се разбира, \(x=2\).

    Сега решете ја равенката: \(3^(x)=8\).Што е x еднакво? Тоа е поентата.

    Најпаметните ќе речат: „Х е нешто помалку од два“. Како точно да се напише овој број? За да се одговори на ова прашање, измислен е логаритам. Благодарение на него, одговорот овде може да се напише како \(x=\log_(3)(8)\).

    Сакам да нагласам дека \(\log_(3)(8)\), како секој логаритам е само број. Да, изгледа необично, но кратко е. Затоа што ако сакаме да го напишеме во форма децимална, тогаш би изгледало вака: \(1.892789260714.....\)

    Пример : Решете ја равенката \(4^(5x-4)=10\)

    Решение :

    \(4^(5x-4)=10\)

    \(4^(5x-4)\) и \(10\) не може да се доведат во истата база. Ова значи дека не можете без логаритам.

    Ајде да ја користиме дефиницијата за логаритам:
    \(a^(b)=c\) \(\лева десна стрелка\) \(\log_(a)(c)=b\)

    \(\log_(4)(10)=5x-4\)

    Ајде да ја превртиме равенката така што X е лево

    \(5x-4=\log_(4)(10)\)

    Пред нас. Ајде да се движиме \(4\) надесно.

    И не плашете се од логаритамот, третирајте го како обичен број.

    \(5x=\log_(4)(10)+4\)

    Поделете ја равенката со 5

    \(x=\)\(\frac(\log_(4)(10)+4)(5)\)

    Ова е нашиот корен. Да, изгледа необично, но тие не го избираат одговорот.

    Одговори : \(\frac(\log_(4)(10)+4)(5)\)

    Децимални и природни логаритми

    Како што е наведено во дефиницијата за логаритам, неговата основа може да биде кој било позитивен број освен еден \((a>0, a\neq1)\). И меѓу сите можни основи, има две кои се појавуваат толку често што е измислена посебна кратка нотација за логаритми со нив:

    Природен логаритам: логаритам чија основа е Ојлеровиот број \(e\) (еднаков на приближно \(2.7182818…\)), а логаритамот е напишан како \(\ln(a)\).

    Тоа е, \(\ln(a)\) е исто како \(\log_(e)(a)\)

    Децимален логаритам: Логаритам чија основа е 10 се пишува \(\lg(a)\).

    Тоа е, \(\lg(a)\) е исто како \(\log_(10)(a)\), каде \(a\) е некој број.

    Основен логаритамски идентитет

    Логаритмите имаат многу својства. Еден од нив се нарекува „Основен логаритамски идентитет“ и изгледа вака:

    \(a^(\log_(a)(c))=c\)

    Ова својство произлегува директно од дефиницијата. Ајде да видиме како точно настанала оваа формула.

    Да се ​​потсетиме на кратка нотација на дефиницијата за логаритам:

    ако \(a^(b)=c\), тогаш \(\log_(a)(c)=b\)

    Тоа е, \(b\) е исто како \(\log_(a)(c)\). Потоа можеме да напишеме \(\log_(a)(c)\) наместо \(b\) во формулата \(a^(b)=c\). Се покажа \(a^(\log_(a)(c))=c\) - главниот логаритамски идентитет.

    Можете да најдете други својства на логаритмите. Со нивна помош, можете да ги поедноставите и пресметате вредностите на изразите со логаритми, кои е тешко директно да се пресметаат.

    Пример : Најдете ја вредноста на изразот \(36^(\log_(6)(5))\)

    Решение :

    Одговори : \(25\)

    Како да напишете број како логаритам?

    Како што споменавме погоре, секој логаритам е само бројка. Обратно е исто така точно: секој број може да се напише како логаритам. На пример, знаеме дека \(\log_(2)(4)\) е еднакво на два. Потоа наместо два можете да напишете \(\log_(2)(4)\).

    Но, \(\log_(3)(9)\) исто така е еднакво на \(2\), што значи дека можеме да напишеме и \(2=\log_(3)(9)\) . Слично со \(\log_(5)(25)\), и со \(\log_(9)(81)\), итн. Тоа е, излегува

    \(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

    Така, ако ни треба, можеме да напишеме два како логаритам со која било основа каде било (било да е тоа во равенка, во израз или во неравенство) - едноставно ја пишуваме основата во квадрат како аргумент.

    Истото е и со тројката - може да се напише како \(\log_(2)(8)\), или како \(\log_(3)(27)\), или како \(\log_(4)( 64) \)... Овде ја пишуваме основата во коцката како аргумент:

    \(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

    И со четири:

    \(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

    И со минус еден:

    \(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\) \(...\)

    И со една третина:

    \(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

    Секој број \(a\) може да се претстави како логаритам со основата \(b\): \(a=\log_(b)(b^(a))\)

    Пример : Најдете го значењето на изразот \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

    Решение :

    Одговори : \(1\)