Chức năng phồng xuống. Tính lồi của hàm số. Hướng lồi. Điểm biến đổi. Điều kiện lồi và uốn. Các tiệm cận của đồ thị hàm số
Khái niệm độ lồi của hàm số
Xét hàm \(y = f\left(x \right),\) được giả sử là liên tục trên khoảng \(\left[ (a,b) \right].\) Hàm \(y = f\ left(x \right )\) được gọi lồi xuống (hoặc đơn giản lồi), nếu với mọi điểm \((x_1)\) và \((x_2)\) từ \(\left[ (a,b) \right]\) thì bất đẳng thức \ Nếu bất đẳng thức này nghiêm ngặt đối với mọi \(( x_1),(x_2) \in \left[ (a,b) \right],\) sao cho \((x_1) \ne (x_2),\) thì hàm \(f\left(x \right) \) được gọi là lồi xuống nghiêm ngặt
Hàm lồi hướng lên được định nghĩa tương tự. Hàm \(f\left(x \right)\) được gọi lồi lên (hoặc lõm), nếu với mọi điểm \((x_1)\) và \((x_2)\) của đoạn \(\left[ (a,b) \right]\) thì bất đẳng thức \ Nếu bất đẳng thức này nghiêm ngặt đối với mọi \ (( x_1),(x_2) \in \left[ (a,b) \right],\) sao cho \((x_1) \ne (x_2),\) thì hàm \(f\left(x \ phải) \) được gọi lồi chặt lên trên trên đoạn \(\left[ (a,b) \right].\)
Giải thích hình học về độ lồi của hàm số
Các định nghĩa được giới thiệu của hàm lồi có cách giải thích hình học đơn giản.
Đối với chức năng, lồi xuống (Hình \(1\)), trung điểm \(B\) của mọi dây \((A_1)(A_2)\) đều nằm cao hơn
Tương tự, đối với hàm lồi lên (Hình \(2\)), trung điểm \(B\) của mọi dây \((A_1)(A_2)\) đều nằm dướiđiểm tương ứng \((A_0)\) của đồ thị hàm số hoặc trùng với điểm này.
Hàm lồi có một thuộc tính trực quan khác liên quan đến vị trí đường tiếp tuyến vào đồ thị của hàm số. Hàm \(f\left(x \right)\) là lồi xuống trên đoạn \(\left[ (a,b) \right]\) khi và chỉ nếu đồ thị của nó nằm không thấp hơn tiếp tuyến được vẽ với nó tại bất kỳ điểm \((x_0)\) nào của đoạn \(\left [ (a ,b) \right]\) (Hình \(3\)).
Theo đó, hàm \(f\left(x \right)\) là lồi lên trên đoạn \(\left[ (a,b) \right]\) khi và chỉ nếu đồ thị của nó nằm không cao hơn tiếp tuyến được vẽ với nó tại bất kỳ điểm \((x_0)\) nào của đoạn \(\left [ (a ,b) \right]\) (Hình \(4\)). Những tính chất này tạo thành một định lý và có thể được chứng minh bằng cách sử dụng định nghĩa về độ lồi của hàm.
Điều kiện đủ để có độ lồi
Giả sử hàm \(f\left(x \right)\) có đạo hàm bậc nhất \(f"\left(x \right)\) tồn tại trên khoảng \(\left[ (a,b) \right], \) và đạo hàm thứ hai \(f""\left(x \right)\) - trên khoảng \(\left((a,b) \right).\) Khi đó các tiêu chí đủ sau đây về độ lồi là hợp lệ:
Nếu \(f""\left(x \right) \ge 0\) với mọi \(x \in \left((a,b) \right),\) thì hàm \(f\left(x \ Phải )\) lồi xuống trên đoạn \(\left[ (a,b) \right];\)
Nếu \(f""\left(x \right) \le 0\) với tất cả \(x \in \left((a,b) \right),\) thì hàm \(f\left(x \ Phải )\) lồi lên trên trên đoạn \(\left[ (a,b) \right].\)
Hãy chứng minh định lý trên cho trường hợp hàm lồi hướng xuống. Cho hàm \(f\left(x \right)\) có đạo hàm bậc hai không âm trên khoảng \(\left((a,b) \right):\) \(f""\left(x \right) \ge 0.\) Chúng ta hãy ký hiệu \((x_0)\) điểm giữa của đoạn \(\left[ ((x_1),(x_2)) \right].\) Giả sử rằng độ dài của đoạn này bằng \(2h.\) Khi đó tọa độ \((x_1)\) và \((x_2)\) có thể được viết là: \[(x_1) = (x_0) - h,\;\; (x_2) = (x_0) + h.\] Chúng ta hãy mở rộng hàm \(f\left(x \right)\) tại điểm \((x_0)\) thành chuỗi Taylor với số hạng còn lại ở dạng Lagrange . Chúng ta nhận được các biểu thức sau: \[ (f\left(((x_1)) \right) = f\left(((x_0) - h) \right) ) = (f\left(((x_0)) \right ) - f"\left(((x_0)) \right)h + \frac((f""\left(((\xi _1)) \right)(h^2)))((2},}
\]
\[
{f\left({{x_2}} \right) = f\left({{x_0} + h} \right) }
= {f\left({{x_0}} \right) + f"\left({{x_0}} \right)h + \frac{{f""\left({{\xi _2}} \right){h^2}}}{{2!}},}
\]
где \({x_0} - h !}
Hãy cộng cả hai đẳng thức: \[ (f\left(((x_1)) \right) + f\left(((x_2)) \right) ) = (2f\left(((x_0)) \right) + \ frac (((h^2)))(2)\left[ (f""\left(((\xi _1)) \right) + f""\left(((\xi _2)) \right) ) \right].) \] Vì \((\xi _1),(\xi _2) \in \left((a,b) \right),\) nên đạo hàm bậc hai ở vế phải là không âm . Do đó, \ hoặc \ tức là theo định nghĩa, hàm \(f\left(x \right)\) lồi xuống
.
Lưu ý rằng điều kiện cần cho độ lồi của một hàm (tức là một định lý trực tiếp trong đó, ví dụ, từ điều kiện lồi trở xuống, nó tuân theo \(f""\left(x \right) \ge 0\)) chỉ được thỏa mãn với các bất đẳng thức không chặt chẽ. Trong trường hợp lồi chặt, điều kiện cần nói chung là không được thỏa mãn. Ví dụ: hàm \(f\left(x \right) = (x^4)\) là hàm lồi hoàn toàn hướng xuống. Tuy nhiên, tại điểm \(x = 0\) đạo hàm bậc hai của nó bằng 0, tức là. bất đẳng thức nghiêm ngặt \(f""\left(x \right) \gt 0\) không đúng trong trường hợp này.
Tính chất của hàm lồi
Chúng ta hãy liệt kê một số tính chất của hàm lồi, giả sử rằng tất cả các hàm đều được xác định và liên tục trên khoảng \(\left[ (a,b) \right].\)
Nếu các hàm \(f\) và \(g\) lồi xuống (hướng lên), thì bất kỳ hàm nào trong số chúng kết hợp tuyến tính \(af + bg,\) trong đó \(a\), \(b\) là các số thực dương, cũng lồi xuống (hướng lên).
Nếu hàm \(u = g\left(x \right)\) lồi xuống và hàm \(y = f\left(u \right)\) lồi xuống và không giảm, thì hàm phức tạp \(y = f\left((g\left(x \right)) \right)\) cũng sẽ lồi xuống.
Nếu hàm \(u = g\left(x \right)\) lồi lên trên và hàm \(y = f\left(u \right)\) lồi xuống và không tăng, thì hàm phức tạp \(y = f\left((g\left(x \right)) \right)\) sẽ lồi xuống.
Tối đa địa phương hàm lồi hướng lên được xác định trên khoảng \(\left[ (a,b) \right],\) cũng là hàm lồi của nó giá trị cao nhất trên phân khúc này.
Tối thiểu địa phương hàm lồi hướng xuống được xác định trên khoảng \(\left[ (a,b) \right],\) cũng là hàm lồi của nó giá trị thấp nhất trên phân khúc này.
Khi vẽ đồ thị hàm số, điều quan trọng là xác định các khoảng lồi và điểm uốn. Chúng ta cần chúng, cùng với các khoảng giảm và tăng, để thể hiện rõ ràng hàm dưới dạng đồ họa.
Để hiểu chủ đề này đòi hỏi kiến thức về đạo hàm của hàm số là gì và cách tính nó theo một thứ tự nào đó, cũng như khả năng giải các loại bất phương trình khác nhau.
Ở đầu bài viết, các khái niệm cơ bản được xác định. Sau đó, chúng ta sẽ chỉ ra mối quan hệ tồn tại giữa hướng của độ lồi và giá trị của đạo hàm bậc hai trong một khoảng nhất định. Tiếp theo, chúng ta sẽ chỉ ra các điều kiện để có thể xác định được điểm uốn của đồ thị. Tất cả các lập luận sẽ được minh họa bằng các ví dụ về giải pháp vấn đề.
Định nghĩa 1Theo hướng đi xuống trong một khoảng nhất định trong trường hợp đồ thị của nó nằm không thấp hơn tiếp tuyến của nó tại bất kỳ điểm nào trong khoảng này.
Định nghĩa 2
Hàm cần lấy vi phân là hàm lồi hướng lên trong một khoảng nhất định nếu đồ thị của hàm số đã cho nằm không cao hơn tiếp tuyến của nó tại bất kỳ điểm nào trong khoảng này.
Hàm lồi hướng xuống cũng có thể được gọi là hàm lõm. Cả hai định nghĩa đều được thể hiện rõ ràng trong biểu đồ dưới đây:
Định nghĩa 3
Điểm uốn của hàm số– đây là điểm M (x 0 ; f (x 0)), tại đó có tiếp tuyến với đồ thị của hàm số, tuân theo sự tồn tại đạo hàm trong lân cận điểm x 0, trong đó ở bên trái và vế phải đồ thị của hàm số có các hướng lồi khác nhau.
Nói một cách đơn giản, điểm uốn là một vị trí trên đồ thị có tiếp tuyến và hướng lồi của đồ thị khi đi qua vị trí này sẽ làm thay đổi hướng của độ lồi. Nếu bạn không nhớ trong những điều kiện nào có thể tồn tại một tiếp tuyến thẳng đứng và không thẳng đứng, chúng tôi khuyên bạn nên lặp lại phần tiếp tuyến của đồ thị hàm số tại một điểm.
Dưới đây là biểu đồ của hàm số có một số điểm uốn được đánh dấu màu đỏ. Hãy để chúng tôi làm rõ rằng sự hiện diện của các điểm uốn là không bắt buộc. Trên đồ thị của một hàm số có thể có một, hai, vài, vô số hoặc không có.
Trong phần này, chúng ta sẽ nói về một định lý mà nhờ đó bạn có thể xác định các khoảng lồi trên đồ thị của một hàm cụ thể.
Định nghĩa 4
Đồ thị của hàm số sẽ lồi hướng xuống hoặc hướng lên nếu hàm tương ứng y = f(x) có đạo hàm hữu hạn bậc hai trên khoảng x đã cho, với điều kiện là bất đẳng thức f "" (x) ≥ 0 ∀ x ∈ X (f "" (x) 0 ∀ x ∈ X) sẽ đúng.
Sử dụng định lý này, bạn có thể tìm thấy các khoảng lõm và lồi trên bất kỳ đồ thị nào của hàm số. Để làm điều này, bạn chỉ cần giải các bất đẳng thức f "" (x) ≥ 0 và f "" (x) 0 trên miền định nghĩa của hàm tương ứng.
Chúng ta hãy làm rõ rằng những điểm mà tại đó đạo hàm bậc hai không tồn tại nhưng hàm y = f (x) được xác định sẽ được đưa vào các khoảng lồi và lõm.
Chúng ta hãy xem một ví dụ về một vấn đề cụ thể để biết cách áp dụng định lý này một cách chính xác.
ví dụ 1
Tình trạng: cho hàm số y = x 3 6 - x 2 + 3 x - 1 . Xác định khoảng thời gian đồ thị của nó có độ lồi và độ lõm.
Giải pháp
Miền định nghĩa của hàm này là toàn bộ tập hợp số thực. Hãy bắt đầu bằng cách tính đạo hàm bậc hai.
y " = x 3 6 - x 2 + 3 x - 1 " = x 2 2 - 2 x + 3 ⇒ y " " = x 2 2 - 2 x + 3 = x - 2
Ta thấy miền định nghĩa của đạo hàm bậc hai trùng với miền của chính hàm số, nghĩa là để xác định các khoảng lồi, ta cần giải các bất đẳng thức f "" (x) ≥ 0 và f "" (x). ) ≤ 0.
y "" ≥ 0 ⇔ x - 2 ≥ 0 ⇔ x ≥ 2 y "" ≤ 0 ⇔ x - 2 ≤ 0 ⇔ x 2
Chúng tôi thấy rằng đồ thị của hàm số đã cho sẽ có độ lõm trên đoạn [2; + ∞) và độ lồi trên đoạn (- ∞; 2 ] .
Để rõ ràng, hãy vẽ đồ thị của hàm số và đánh dấu phần lồi bằng màu xanh lam và phần lõm bằng màu đỏ.
Trả lời:đồ thị của hàm số đã cho sẽ có độ lõm trên đoạn [ 2 ; + ∞) và độ lồi trên đoạn (- ∞; 2 ] .
Nhưng phải làm gì nếu miền định nghĩa của đạo hàm bậc hai không trùng với miền định nghĩa của hàm số? Ở đây nhận xét được đưa ra ở trên sẽ hữu ích cho chúng ta: chúng ta cũng sẽ bao gồm những điểm mà đạo hàm bậc hai hữu hạn không tồn tại trong các đoạn lõm và lồi.
Ví dụ 2
Tình trạng: cho hàm số y = 8 x x - 1 . Xác định trong khoảng thời gian nào đồ thị của nó sẽ lõm và trong khoảng thời gian nào nó sẽ lồi.
Giải pháp
Đầu tiên, chúng ta hãy tìm ra miền định nghĩa của hàm.
x ≥ 0 x - 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [ 0 ; 1) ∪ (1 ; + ∞)
Bây giờ chúng ta tính đạo hàm bậc hai:
y " = 8 x x - 1 " = 8 1 2 x (x - 1) - x 1 (x - 1) 2 = - 4 x + 1 x (x - 1) 2 y "" = - 4 x + 1 x (x - 1) 2 " = - 4 1 x x - 1 2 - (x + 1) x x - 1 2 " x (x - 1) 4 = = - 4 1 x x - 1 2 - x + 1 1 2 x ( x - 1) 2 + x 2 (x - 1) x x - 1 4 = = 2 3 x 2 + 6 x - 1 x 3 2 · (x - 1) 3
Miền định nghĩa của đạo hàm bậc hai là tập x ∈ (0 ; 1) ∪ (1 ; + ∞) . Ta thấy rằng x bằng 0 sẽ thuộc miền của hàm số ban đầu chứ không thuộc miền của đạo hàm bậc hai. Điểm này phải được bao gồm trong đoạn lõm hoặc lồi.
Sau đó, chúng ta cần giải các bất đẳng thức f "" (x) ≥ 0 và f "" (x) ≤ 0 trên miền định nghĩa của hàm đã cho. Chúng ta sử dụng phương pháp khoảng cho việc này: với x = - 1 - 2 3 3 ≈ - 2, 1547 hoặc x = - 1 + 2 3 3 ≈ 0, 1547 tử số 2 · (3 x 2 + 6 x - 1) x 2 3 · x - 1 3 trở thành 0 và mẫu số là 0 khi x bằng 0 hoặc một.
Hãy vẽ các điểm kết quả trên biểu đồ và xác định dấu của biểu thức trên tất cả các khoảng sẽ nằm trong miền định nghĩa của hàm ban đầu. Khu vực này được biểu thị bằng cách tô bóng trên biểu đồ. Nếu giá trị là dương, chúng ta đánh dấu khoảng bằng dấu cộng, nếu âm thì bằng dấu trừ.
Kể từ đây,
f "" (x) ≥ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ 0 ; - 1 + 2 3 3 ∪ (1 ; + ∞) , và f "" (x) ≤ 0 x ∈ [ 0 ; 1) ∪ (1 ; + ∞) ⇔ x ∈ [ - 1 + 2 3 3 ; 1)
Chúng tôi bao gồm điểm được đánh dấu trước đó x = 0 và nhận được câu trả lời mong muốn. Đồ thị của hàm số ban đầu sẽ lồi xuống tại 0; - 1 + 2 3 3 ∪ (1 ; + ∞) , và trở lên – với x ∈ [ - 1 + 2 3 3 ; 1) .
Hãy vẽ biểu đồ, đánh dấu phần lồi màu xanh lam và phần lõm màu đỏ. Đường tiệm cận đứng được đánh dấu bằng một đường chấm màu đen.
Trả lời:Đồ thị của hàm số ban đầu sẽ lồi xuống tại 0; - 1 + 2 3 3 ∪ (1 ; + ∞) , và trở lên – với x ∈ [ - 1 + 2 3 3 ; 1) .
Điều kiện uốn của đồ thị hàm số
Hãy bắt đầu bằng cách xây dựng điều kiện cần thiết cho sự uốn của đồ thị của một hàm số nhất định.
Định nghĩa 5
Giả sử chúng ta có hàm y = f (x), đồ thị của hàm này có điểm uốn. Tại x = x 0 nó có đạo hàm bậc hai liên tục, do đó đẳng thức f "" (x 0) = 0 sẽ giữ nguyên.
Với điều kiện này, chúng ta nên tìm các điểm uốn trong số những điểm mà tại đó đạo hàm bậc hai sẽ chuyển về 0. Điều kiện này sẽ không đủ: không phải tất cả những điểm như vậy đều phù hợp với chúng ta.
Cũng lưu ý rằng, theo định nghĩa chung, chúng ta sẽ cần một đường tiếp tuyến, thẳng đứng hoặc không thẳng đứng. Trong thực tế, điều này có nghĩa là để tìm các điểm uốn, bạn nên lấy những điểm mà tại đó đạo hàm bậc hai của một hàm số đã cho chuyển về 0. Do đó, để tìm hoành độ của các điểm uốn, ta cần lấy tất cả x 0 từ miền định nghĩa của hàm số, trong đó lim x → x 0 - 0 f " (x) = ∞ và lim x → x 0 + 0 f" (x) = ∞. Thông thường, đây là những điểm mà tại đó mẫu số của đạo hàm bậc nhất trở thành 0.
Điều kiện đủ đầu tiên để tồn tại điểm uốn trong đồ thị hàm số
Chúng tôi đã tìm thấy tất cả các giá trị của x 0 có thể được coi là hoành độ của các điểm uốn. Sau đó, chúng ta cần áp dụng điều kiện uốn đủ đầu tiên.
Định nghĩa 6
Giả sử chúng ta có hàm y = f (x) liên tục tại điểm M (x 0 ; f (x 0)). Hơn nữa, nó có tiếp tuyến tại điểm này và bản thân hàm số có đạo hàm bậc hai ở gần điểm này x 0. Trong trường hợp này, nếu ở bên trái và bên phải, đạo hàm bậc hai thu được dấu ngược nhau, thì điểm này có thể được coi là điểm uốn.
Chúng ta thấy rằng điều kiện này không đòi hỏi đạo hàm bậc hai nhất thiết phải tồn tại ở điểm này; sự hiện diện của nó ở lân cận điểm x 0 là đủ.
Thật thuận tiện khi trình bày mọi thứ đã nói ở trên dưới dạng một chuỗi hành động.
- Trước tiên, bạn cần tìm tất cả hoành độ x 0 của các điểm uốn có thể có, trong đó f "" (x 0) = 0, lim x → x 0 - 0 f " (x) = ∞, lim x → x 0 + 0 f " (x) = ∞ .
- Hãy tìm xem đạo hàm sẽ đổi dấu tại điểm nào. Các giá trị này là hoành độ của các điểm uốn và các điểm M (x 0 ; f (x 0)) tương ứng với chúng chính là các điểm uốn.
Để rõ ràng, chúng tôi sẽ phân tích hai vấn đề.
Ví dụ 3
Tình trạng: cho hàm số y = 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x. Xác định nơi đồ thị của hàm số này sẽ có điểm uốn và điểm lồi.
Giải pháp
Hàm đã chỉ định được xác định trên toàn bộ tập hợp số thực. Chúng tôi tính toán đạo hàm đầu tiên:
y" = 1 10 x 4 12 - x 3 6 - 3 x 2 + 2 x " = 1 10 4 x 3 12 - 3 x 2 6 - 6 x + 2 = = 1 10 x 3 3 - x 2 2 - 6 x + 2
Bây giờ chúng ta hãy tìm miền định nghĩa của đạo hàm bậc nhất. Nó cũng là tập hợp tất cả các số thực. Điều này có nghĩa là các đẳng thức lim x → x 0 - 0 f " (x) = ∞ và lim x → x 0 + 0 f " (x) = ∞ không thể thỏa mãn với bất kỳ giá trị nào của x 0 .
Chúng tôi tính đạo hàm thứ hai:
y " " = = 1 10 · x 3 3 - x 2 2 - 6 x + 2 " = 1 10 · 3 x 2 3 - 2 x 2 - 6 = 1 10 · x 2 - x - 6
y "" = 0 ⇔ 1 10 · (x 2 - x - 6) = 0 ⇔ x 2 - x - 6 = 0 D = (- 1) 2 - 4 · 1 · (- 6) = 25 x 1 = 1 - 25 2 = - 2, x 2 = 1 + 25 2 = 3
Chúng tôi đã tìm thấy trục hoành của hai điểm uốn có thể có - 2 và 3. Tất cả những gì còn lại chúng ta phải làm là kiểm tra xem đạo hàm đổi dấu tại điểm nào. Hãy vẽ một trục số và vẽ các điểm này trên đó, sau đó chúng ta sẽ đặt dấu của đạo hàm bậc hai trên các khoảng kết quả.
Các cung thể hiện hướng lồi của đồ thị trong mỗi khoảng.
Đạo hàm bậc hai đổi dấu ngược lại (từ cộng sang trừ) tại điểm có hoành độ 3, đi qua nó từ trái sang phải và cũng thực hiện điều này (từ trừ sang dương) tại điểm có hoành độ 3. Điều này có nghĩa là chúng ta có thể kết luận rằng x = - 2 và x = 3 là hoành độ của các điểm uốn của đồ thị hàm số. Chúng sẽ tương ứng với các điểm biểu đồ - 2; - 4 3 và 3; - 15 8 .
Chúng ta hãy quan sát lại hình ảnh trục số và các dấu kết quả ở các khoảng để rút ra kết luận về vị trí lồi, lõm. Hóa ra độ lồi sẽ nằm trên đoạn - 2; 3, và độ lõm trên các đoạn (- ∞; - 2 ] và [ 3; + ∞).
Lời giải của bài toán được thể hiện rõ ràng trên đồ thị: màu xanh biểu thị độ lồi, màu đỏ biểu thị độ lõm, màu đen biểu thị điểm uốn.
Trả lời:độ lồi sẽ nằm trên đoạn - 2; 3, và độ lõm trên các đoạn (- ∞; - 2 ] và [ 3; + ∞).
Ví dụ 4
Tình trạng: tính hoành độ của tất cả các điểm uốn của đồ thị hàm số y = 1 8 · x 2 + 3 x + 2 · x - 3 3 5 .
Giải pháp
Miền định nghĩa của một hàm số đã cho là tập hợp tất cả các số thực. Chúng tôi tính toán đạo hàm:
y " = 1 8 · (x 2 + 3 x + 2) · x - 3 3 5 " = = 1 8 · x 2 + 3 x + 2 " · (x - 3) 3 5 + (x 2 + 3 x + 2) x - 3 3 5 " = = 1 8 2 x + 3 (x - 3) 3 5 + (x 2 + 3 x + 2) 3 5 x - 3 - 2 5 = 13 x 2 - 6 x - 39 40 · (x - 3) 2 5
Không giống như một hàm số, đạo hàm cấp một của nó sẽ không được xác định ở giá trị x bằng 3, nhưng:
lim x → 3 - 0 y " (x) = 13 · (3 - 0) 2 - 6 · (3 - 0) - 39 40 · 3 - 0 - 3 2 5 = + ∞ lim x → 3 + 0 y " (x) = 13 · (3 + 0) 2 - 6 · (3 + 0) - 39 40 · 3 + 0 - 3 2 5 = + ∞
Điều này có nghĩa là một tiếp tuyến dọc của đồ thị sẽ đi qua điểm này. Vì vậy, 3 có thể là hoành độ của điểm uốn.
Chúng tôi tính toán đạo hàm thứ hai. Chúng ta cũng tìm được miền xác định của nó và các điểm tại đó nó chuyển về 0:
y "" = 13 x 2 - 6 x - 39 40 x - 3 2 5 " = = 1 40 13 x 2 - 6 x - 39 " (x - 3) 2 5 - 13 x 2 - 6 x - 39 · x - 3 2 5 " (x - 3) 4 5 = = 1 25 · 13 x 2 - 51 x + 21 (x - 3) 7 5 , x ∈ (- ∞ ; 3) ∪ (3 ; + ∞ ) y " " (x) = 0 ⇔ 13 x 2 - 51 x + 21 = 0 D = (- 51) 2 - 4 13 21 = 1509 x 1 = 51 + 1509 26 ≈ 3, 4556, x 2 = 51 - 1509 26 ≈ 0,4675
Bây giờ chúng ta có thêm hai điểm uốn có thể xảy ra. Hãy vẽ tất cả chúng trên trục số và đánh dấu các khoảng kết quả bằng các dấu hiệu:
Dấu hiệu sẽ thay đổi khi đi qua từng điểm được chỉ định, nghĩa là chúng đều là điểm uốn.
Trả lời: Hãy vẽ đồ thị của hàm số, đánh dấu các phần lõm màu đỏ, phần lồi màu xanh lam và các điểm uốn màu đen:
Biết điều kiện đủ thứ nhất cho sự uốn, chúng ta có thể xác định các điểm cần thiết mà tại đó không cần có đạo hàm bậc hai. Dựa trên điều này, điều kiện đầu tiên có thể được coi là phổ biến nhất và phù hợp để giải quyết các loại vấn đề khác nhau.
Lưu ý rằng còn có hai điều kiện uốn nữa nhưng chúng chỉ có thể được áp dụng khi có đạo hàm hữu hạn tại điểm đã xác định.
Nếu ta có f "" (x 0) = 0 và f """ (x 0) ≠ 0 thì x 0 sẽ là hoành độ của điểm uốn của đồ thị y = f(x).
Ví dụ 5
Tình trạng:đã cho hàm số y = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5. Xác định xem đồ thị của hàm số có điểm uốn tại điểm 3 hay không; 4 5 .
Giải pháp
Điều đầu tiên cần làm là đảm bảo rằng điểm này thường thuộc đồ thị của hàm này.
y (3) = 1 60 3 3 - 3 20 3 2 - 2 5 = 27 60 - 27 20 + 21 10 - 2 5 = 9 - 27 + 42 - 8 20 = 4 5
Hàm đã cho được xác định cho tất cả các đối số là số thực. Hãy tính đạo hàm bậc nhất và bậc hai:
y" = 1 60 x 3 - 3 20 x 2 + 7 10 x - 2 5 " = 1 20 x 2 - 3 10 x + 7 10 y "" = 1 20 x 2 - 3 10 x + 7 10 " = 1 10 x - 3 10 = 1 10 (x - 3)
Chúng tôi thấy rằng đạo hàm bậc hai sẽ tiến về 0 nếu x bằng 0. Điều này có nghĩa là điều kiện uốn cần thiết cho điểm này sẽ được thỏa mãn. Bây giờ chúng ta sử dụng điều kiện thứ hai: tìm đạo hàm thứ ba và tìm xem liệu nó có chuyển về 0 tại 3 hay không:
y " " " = 1 10 (x - 3) " = 1 10
Đạo hàm bậc ba sẽ không biến mất đối với bất kỳ giá trị nào của x. Do đó, chúng ta có thể kết luận điểm này sẽ là điểm uốn của đồ thị hàm số.
Trả lời: Hãy thể hiện giải pháp trong hình minh họa:
Giả sử f "(x 0) = 0, f "" (x 0) = 0, ..., f (n) (x 0) = 0 và f (n + 1) (x 0) ≠ 0 . Trong trường hợp này, với n chẵn, ta thu được x 0 là hoành độ của điểm uốn của đồ thị y = f(x).
Ví dụ 6
Tình trạng: cho hàm y = (x - 3) 5 + 1. Tính điểm uốn của đồ thị của nó.
Giải pháp
Hàm này được xác định trên toàn bộ tập số thực. Chúng ta tính đạo hàm: y " = ((x - 3) 5 + 1) " = 5 x - 3 4 . Vì nó cũng sẽ được xác định cho tất cả các giá trị thực của đối số, nên một tiếp tuyến không thẳng đứng sẽ tồn tại tại bất kỳ điểm nào trong biểu đồ của nó.
Bây giờ hãy tính xem đạo hàm bậc hai sẽ chuyển về 0 ở những giá trị nào:
y "" = 5 · (x - 3) 4 " = 20 · x - 3 3 y "" = 0 ⇔ x - 3 = 0 ⇔ x = 3
Ta thấy rằng tại x = 3 đồ thị của hàm số có thể có một điểm uốn. Hãy sử dụng điều kiện thứ ba để xác nhận điều này:
y " " " = 20 · (x - 3) 3 " = 60 · x - 3 2 , y " " " (3) = 60 · 3 - 3 2 = 0 y (4) = 60 · (x - 3) 2 " = 120 · (x - 3) , y (4) (3) = 120 · (3 - 3) = 0 y (5) = 120 · (x - 3) " = 120 , y (5) (3 ) = 120 ≠ 0
Ta có n = 4 theo điều kiện đủ thứ ba. Đây là số chẵn, nghĩa là x = 3 sẽ là hoành độ của điểm uốn và điểm đồ thị của hàm (3; 1) tương ứng với nó.
Trả lời:Đây là đồ thị của hàm này với các độ lồi, độ lõm và điểm uốn được đánh dấu:
Nếu bạn thấy văn bản có lỗi, vui lòng đánh dấu nó và nhấn Ctrl+Enter
Đồ thị của hàm số y=f(x) gọi điện lồi trên khoảng thời gian (a; b), nếu nó nằm bên dưới bất kỳ tiếp tuyến nào của nó trên khoảng này.
Đồ thị của hàm số y=f(x) gọi điện lõm trên khoảng thời gian (a; b), nếu nó nằm phía trên bất kỳ tiếp tuyến nào của nó trong khoảng này.
Hình vẽ cho thấy một đường cong lồi tại (a; b) và lõm trên (b;c).
Ví dụ.
Chúng ta hãy xem xét một tiêu chí đủ cho phép chúng ta xác định xem đồ thị của hàm số trong một khoảng nhất định sẽ là lồi hay lõm.
Định lý. Cho phép y=f(x) có thể phân biệt bằng (a; b). Nếu tại mọi điểm của khoảng (a; b)đạo hàm bậc hai của hàm y = f(x) tiêu cực, tức là f ""(x) < 0, то график функции на этом интервале выпуклый, если же f""(x) > 0 – lõm.
Bằng chứng. Chúng ta hãy giả định một cách chắc chắn rằng f""(x) < 0 и докажем, что график функции будет выпуклым.
Hãy lấy các hàm trên đồ thị y = f(x)điểm tùy ý M0 với cơ hoành x 0 Î ( Một; b) và vẽ qua điểm M0đường tiếp tuyến. Phương trình của cô ấy. Ta phải chứng minh rằng đồ thị của hàm số trên (a; b) nằm bên dưới tiếp tuyến này, tức là ở cùng một giá trị x tọa độ của đường cong y = f(x) sẽ nhỏ hơn tọa độ của tiếp tuyến.
Vậy phương trình của đường cong là y = f(x). Chúng ta hãy biểu thị tọa độ của tiếp tuyến tương ứng với hoành độ x. Sau đó . Do đó, sự khác biệt giữa tọa độ của đường cong và tiếp tuyến cho cùng một giá trị x sẽ .
Sự khác biệt f(x) – f(x 0) biến đổi theo định lý Lagrange, trong đó c giữa x Và x 0.
Như vậy,
Chúng ta lại áp dụng định lý Lagrange cho biểu thức trong ngoặc vuông: , trong đó c 1 giữa c 0 Và x 0. Theo điều kiện của định lý f ""(x) < 0. Определим знак произведения второго и третьего сомножителей.
Do đó, bất kỳ điểm nào trên đường cong đều nằm dưới tiếp tuyến của đường cong đối với mọi giá trị x Và x 0 Î ( Một; b), có nghĩa là đường cong lồi. Phần thứ hai của định lý được chứng minh theo cách tương tự.
Ví dụ.
Điểm trên đồ thị của hàm số liên tục ngăn cách phần lồi của nó với phần lõm được gọi là điểm uốn.
Rõ ràng, tại điểm uốn, tiếp tuyến, nếu tồn tại, sẽ cắt đường cong, bởi vì ở một phía của điểm này, đường cong nằm dưới tiếp tuyến và ở phía bên kia - phía trên nó.
Chúng ta hãy xác định các điều kiện đủ để một điểm cho trước của đường cong là một điểm uốn.
Định lý. Hãy để đường cong được xác định bởi phương trình y = f(x). Nếu như f ""(x 0) = 0 hoặc f ""(x 0) không tồn tại ngay cả khi truyền qua giá trị x = x 0 phát sinh f ""(x) đổi dấu thì điểm trên đồ thị của hàm số với hoành độ x = x 0 có một điểm uốn.
Bằng chứng. Cho phép f ""(x) < 0 при x < x 0 Và f ""(x) > 0 tại x > x 0. Sau đó tại x < x 0đường cong lồi và khi x > x 0– lõm. Vì vậy, điểm MỘT, nằm trên đường cong, có cơ bụng x 0 có một điểm uốn. Trường hợp thứ hai có thể xét tương tự khi f ""(x) > 0 tại x < x 0 Và f ""(x) < 0 при x > x 0.
Vì vậy, các điểm uốn chỉ nên tìm trong số những điểm mà đạo hàm bậc hai triệt tiêu hoặc không tồn tại.
Ví dụ. Tìm các điểm uốn và xác định các khoảng lồi, lõm của các đường cong.
CÁC TÍN HIỆU CỦA ĐỒ HỌA HÀM
Khi nghiên cứu một hàm số, điều quan trọng là thiết lập hình dạng của đồ thị của nó ở khoảng cách không giới hạn từ điểm đồ thị đến gốc tọa độ.
Điều đặc biệt quan tâm là trường hợp khi đồ thị của một hàm số, khi điểm biến của nó bị loại bỏ đến vô cùng, tiến vô thời hạn đến một đường thẳng nhất định.
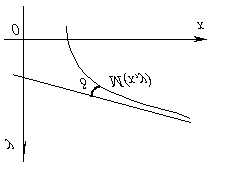
Đường thẳng được gọi là đường tiệm cậnđồ họa chức năng y = f(x), nếu khoảng cách từ điểm biến Mđồ họa vào dòng này khi xóa một điểm Mđến vô cùng có xu hướng bằng không, tức là một điểm trên đồ thị của một hàm số, vì nó có xu hướng tiến tới vô cùng, phải tiến tới tiệm cận vô hạn một cách vô hạn.
Một đường cong có thể tiến tới tiệm cận của nó, ở một phía của nó hoặc ở các phía khác nhau, đi qua tiệm cận vô số lần và di chuyển từ phía này sang phía bên kia.
Nếu chúng ta biểu thị bằng d khoảng cách từ điểm Mđường cong tới tiệm cận thì rõ ràng d có xu hướng bằng 0 khi điểm di chuyển ra xa Mđến vô cùng.
Chúng ta sẽ phân biệt rõ hơn giữa các tiệm cận đứng và tiệm cận xiên.
CÁC ASYMPTOTES DỌC
Hãy để tại x→ x 0 từ bất kỳ chức năng bên nào y = f(x) tăng vô hạn về giá trị tuyệt đối, tức là hoặc hoặc 
. Khi đó từ định nghĩa đường tiệm cận suy ra rằng đường thẳng x = x 0 là một tiệm cận. Điều ngược lại cũng hiển nhiên nếu đường x = x 0 là một tiệm cận, tức là .
Như vậy, tiệm cận đứng của đồ thị hàm số y = f(x)được gọi là đường thẳng nếu f(x)→ ∞ theo ít nhất một trong các điều kiện x→ x 0– 0 hoặc x → x 0 + 0, x = x 0
Do đó, để tìm các tiệm cận đứng của đồ thị hàm số y = f(x) cần tìm những giá trị đó x = x 0, tại đó hàm số tiến tới vô cùng (có sự gián đoạn vô hạn). Khi đó tiệm cận đứng có phương trình x = x 0.
Ví dụ.
TIỆN LỢI NGHỈ
Vì tiệm cận là một đường thẳng nên nếu đường cong y = f(x) có một tiệm cận xiên thì phương trình của nó sẽ là y = kx + b. Nhiệm vụ của chúng ta là tìm các hệ số k Và b.
Định lý. Thẳng y = kx + bđóng vai trò là một tiệm cận xiên tại x→ +∞ cho đồ thị của hàm số y
= f(x) khi đó và chỉ khi nào 
. Một tuyên bố tương tự là đúng cho x → –∞.
Bằng chứng. Cho phép nghị sĩ- độ dài của đoạn thẳng bằng khoảng cách từ điểm đó Mđến tiệm cận. Theo điều kiện. Chúng ta hãy biểu thị bằng φ góc nghiêng của đường tiệm cận với trục Con bò đực. Sau đó từ ∆MNP theo sau đó. Vì φ là một góc không đổi (φ ≠ π/2), nên , nhưng
Khi nghiên cứu một hàm số và xây dựng đồ thị của nó, ở một giai đoạn chúng ta xác định các điểm uốn và các khoảng lồi. Những dữ liệu này, cùng với các khoảng tăng và giảm, giúp biểu diễn dưới dạng sơ đồ đồ thị của hàm đang nghiên cứu.
Phần trình bày tiếp theo giả định rằng bạn có thể thực hiện tối đa một số đơn đặt hàng và các loại khác nhau.
Hãy bắt đầu nghiên cứu tài liệu với các định nghĩa và khái niệm cần thiết. Tiếp theo, chúng ta sẽ nói về mối liên hệ giữa giá trị đạo hàm bậc hai của một hàm trên một khoảng nhất định và hướng lồi của nó. Sau đó, chúng ta hãy chuyển sang các điều kiện cho phép chúng ta xác định các điểm uốn của đồ thị hàm số. Xuyên suốt bài viết chúng tôi sẽ đưa ra những ví dụ điển hình kèm theo giải pháp chi tiết.
Điều hướng trang.
Tính lồi, tính lõm của hàm số, điểm uốn.
Sự định nghĩa.
lồi xuống trên khoảng X nếu đồ thị của nó nằm không thấp hơn tiếp tuyến với nó tại bất kỳ điểm nào của khoảng X.
Sự định nghĩa.
Hàm cần lấy vi phân được gọi là lồi lên trên khoảng X nếu đồ thị của nó nằm không cao hơn tiếp tuyến của nó tại bất kỳ điểm nào trong khoảng X.
Hàm lồi hướng lên thường được gọi là lồi, và lồi xuống – lõm.
Nhìn vào hình vẽ minh họa các định nghĩa này.
Sự định nghĩa.
Điểm đó được gọi là điểm uốn của đồ thị hàm số y=f(x) nếu tại một điểm cho trước có một tiếp tuyến với đồ thị của hàm số (nó có thể song song với trục Oy) và có một lân cận của điểm nằm bên trái và bên phải của điểm M đồ thị của hàm số có các hướng lồi khác nhau.
Nói cách khác, điểm M được gọi là điểm uốn của đồ thị hàm số nếu có một tiếp tuyến tại điểm này và đồ thị của hàm thay đổi hướng của lồi, đi qua nó.
Nếu cần, hãy tham khảo phần để nhớ lại các điều kiện tồn tại của tiếp tuyến không thẳng đứng và tiếp tuyến thẳng đứng.
Hình dưới đây cho thấy một số ví dụ về điểm uốn (được đánh dấu bằng các chấm màu đỏ). Lưu ý rằng một số hàm có thể không có điểm uốn, trong khi những hàm khác có thể có một, một số hoặc vô số điểm uốn.
Tìm khoảng lồi của hàm số.
Chúng ta hãy xây dựng một định lý cho phép chúng ta xác định các khoảng lồi của một hàm số.
Định lý.
Nếu hàm y=f(x) có đạo hàm bậc hai hữu hạn trên khoảng X và nếu bất đẳng thức đúng 
(), thì đồ thị của hàm số có độ lồi hướng xuống (hướng lên) bởi X.
Định lý này cho phép bạn tìm các khoảng lõm và lồi của một hàm; bạn chỉ cần giải các bất đẳng thức và tương ứng trên miền định nghĩa của hàm ban đầu.
Cần lưu ý rằng các điểm tại đó hàm y=f(x) được xác định và đạo hàm bậc hai không tồn tại sẽ được đưa vào các khoảng lõm và lồi.
Hãy hiểu điều này bằng một ví dụ.
Ví dụ.
Tìm các khoảng mà đồ thị hàm số 
có độ lồi hướng lên trên và độ lồi hướng xuống dưới.
Giải pháp.
Miền xác định của hàm số là toàn bộ tập hợp số thực.
Hãy tìm đạo hàm thứ hai. 
Miền định nghĩa của đạo hàm bậc hai trùng với miền định nghĩa của hàm số ban đầu, do đó, để tìm ra các khoảng lồi, lõm chỉ cần giải và theo đó là đủ. 
Do đó, hàm số lồi xuống trên khoảng và lồi lên trên khoảng .
Minh họa đồ họa.
Phần của đồ thị hàm số trong khoảng lồi được hiển thị bằng màu xanh lam và trong khoảng lõm – có màu đỏ.
Bây giờ hãy xem xét một ví dụ khi miền định nghĩa của đạo hàm bậc hai không trùng với miền định nghĩa của hàm số. Trong trường hợp này, như chúng ta đã lưu ý, các điểm trong miền định nghĩa tại đó không tồn tại đạo hàm bậc hai hữu hạn nên được đưa vào các khoảng lồi và (hoặc) lõm.
Ví dụ.
Tìm các khoảng lồi và lõm của đồ thị hàm số.
Giải pháp.
Hãy bắt đầu với miền của hàm:
Hãy tìm đạo hàm thứ hai: 
Miền định nghĩa của đạo hàm bậc hai là tập hợp 
. Như bạn có thể thấy, x=0 thuộc miền của hàm số ban đầu, nhưng không thuộc miền của đạo hàm bậc hai. Đừng quên điểm này; nó sẽ cần phải được đưa vào khoảng lồi và (hoặc) lõm.
Bây giờ chúng ta giải các bất đẳng thức trên miền định nghĩa của hàm ban đầu. Hãy nộp đơn. Tử số của biểu thức 
tiến tới 0 tại 
hoặc 
, mẫu số – tại x = 0 hoặc x = 1. Chúng tôi vẽ sơ đồ các điểm này trên trục số và tìm ra dấu của biểu thức trên mỗi khoảng có trong miền định nghĩa của hàm ban đầu (nó được hiển thị dưới dạng vùng bóng mờ trên trục số phía dưới). Đối với giá trị dương, chúng ta đặt dấu cộng, đối với giá trị âm, chúng ta đặt dấu trừ. 
Như vậy,
Và 
Do đó, bằng cách đưa điểm x=0 vào, chúng ta sẽ có câu trả lời.
Tại 
đồ thị của hàm số có độ lồi hướng xuống dưới, với 
- độ lồi hướng lên trên.
Minh họa đồ họa.
Phần đồ thị của hàm số trên khoảng lồi được mô tả bằng màu xanh lam, trên các khoảng lõm - màu đỏ, đường chấm màu đen là tiệm cận đứng.
Điều kiện cần và đủ để uốn.
Điều kiện cần để uốn.
Hãy xây dựng điều kiện cần để uốnđồ họa chức năng.
Giả sử đồ thị của hàm y=f(x) uốn tại một điểm và có đạo hàm bậc hai liên tục thì đẳng thức giữ nguyên.
Từ điều kiện này, nó suy ra rằng trục hoành của các điểm uốn phải được tìm trong số những điểm mà tại đó đạo hàm bậc hai của hàm số biến mất. NHƯNG, điều kiện này là không đủ, nghĩa là không phải tất cả các giá trị trong đó đạo hàm bậc hai bằng 0 đều là hoành độ của các điểm uốn.
Cũng cần lưu ý rằng định nghĩa về điểm uốn đòi hỏi sự tồn tại của một đường tiếp tuyến hoặc một đường thẳng đứng. Điều đó có nghĩa là gì? Và điều này có nghĩa như sau: hoành độ của các điểm uốn có thể là mọi thứ từ miền định nghĩa của hàm mà theo đó 
Và 
. Đây thường là những điểm mà tại đó mẫu số của đạo hàm bậc nhất biến mất.
Điều kiện đủ thứ nhất để uốn.
Sau khi tất cả những gì có thể là điểm uốn đã được tìm thấy, bạn nên sử dụng điều kiện đủ thứ nhất để uốnđồ họa chức năng.
Giả sử hàm y=f(x) liên tục tại một điểm, có một tiếp tuyến (có thể thẳng đứng) tại nó, và để hàm này có đạo hàm bậc hai trong một lân cận nào đó của điểm. Khi đó, nếu trong vùng lân cận bên trái và bên phải của , đạo hàm bậc hai có dấu khác nhau thì đó là điểm uốn trong đồ thị của hàm số.
Như bạn có thể thấy, điều kiện đủ thứ nhất không yêu cầu sự tồn tại của đạo hàm thứ hai tại chính điểm đó, nhưng yêu cầu sự tồn tại của nó trong lân cận của điểm.
Bây giờ hãy tóm tắt tất cả thông tin dưới dạng thuật toán.
Thuật toán tìm điểm uốn của hàm số.
Chúng tôi tìm thấy tất cả các điểm uốn có thể có của đồ thị hàm số (hoặc Và ) và tìm ra bằng cách đi qua đạo hàm bậc hai đổi dấu. Các giá trị như vậy sẽ là hoành độ của các điểm uốn và các điểm tương ứng sẽ là điểm uốn của đồ thị hàm số.
Hãy xem xét hai ví dụ về việc tìm điểm uốn để làm rõ.
Ví dụ.
Tìm các điểm uốn và các khoảng lồi, lõm của đồ thị hàm số.
Giải pháp.
Miền xác định của hàm số là toàn bộ tập hợp số thực.
Hãy tìm đạo hàm bậc nhất:
Miền định nghĩa của đạo hàm bậc nhất cũng là toàn bộ tập số thực, do đó các đẳng thức Và không được đáp ứng cho bất kỳ .
Hãy tìm đạo hàm thứ hai:
Hãy cùng tìm hiểu xem giá trị nào của đối số x đạo hàm bậc hai bằng 0: 
Do đó, hoành độ của các điểm uốn có thể là x=-2 và x=3.
Bây giờ vẫn còn phải kiểm tra, sử dụng một dấu uốn vừa đủ, tại điểm nào trong số các điểm này đạo hàm bậc hai thay đổi dấu. Để làm điều này, hãy vẽ các điểm x=-2 và x=3 trên trục số và, như trong phương pháp khoảng tổng quát, chúng ta đặt dấu của đạo hàm bậc hai trên mỗi khoảng. Trong mỗi khoảng, hướng lồi của đồ thị hàm số được thể hiện dưới dạng sơ đồ bằng các cung. 
Đạo hàm bậc hai đổi dấu từ cộng sang trừ, đi qua điểm x=-2 từ trái sang phải và đổi dấu từ âm sang dương, đi qua x=3. Do đó, cả x=-2 và x=3 đều là hoành độ của các điểm uốn của đồ thị hàm số. Chúng tương ứng với các điểm đồ thị và .
Nhìn lại trục số và dấu của đạo hàm bậc hai trên các khoảng của nó, chúng ta có thể rút ra kết luận về các khoảng lồi và lõm. Đồ thị của hàm số lồi trên khoảng và lõm trên các khoảng và .
Minh họa đồ họa.
Phần của đồ thị hàm số trên khoảng lồi được hiển thị bằng màu xanh lam, trên khoảng lõm – có màu đỏ và các điểm uốn được hiển thị dưới dạng các chấm đen.
Ví dụ.
Tìm hoành độ của tất cả các điểm uốn của đồ thị hàm số 
.
Giải pháp.
Miền định nghĩa của hàm này là toàn bộ tập hợp số thực.
Hãy tìm đạo hàm. 
Đạo hàm bậc nhất, không giống như hàm số ban đầu, không được xác định tại x=3. Nhưng 
Và 
. Do đó, tại điểm có trục hoành x=3 có một tiếp tuyến thẳng đứng với đồ thị của hàm số ban đầu. Do đó, x=3 có thể là hoành độ của điểm uốn của đồ thị hàm số.
Chúng ta tìm đạo hàm bậc hai, phạm vi định nghĩa của nó và các điểm mà tại đó nó triệt tiêu: 
Chúng tôi thu được thêm hai trục hoành của các điểm uốn. Chúng tôi đánh dấu cả ba điểm trên trục số và xác định dấu của đạo hàm bậc hai trên mỗi khoảng kết quả. 
Đạo hàm bậc hai đổi dấu khi đi qua từng điểm nên đều là trục hoành của các điểm uốn.
Minh họa đồ họa.
Các phần của đồ thị hàm số được hiển thị bằng màu xanh lam tại các khoảng lồi, màu đỏ tại các khoảng lõm và các điểm uốn được hiển thị dưới dạng các chấm đen.
Điều kiện đủ đầu tiên cho sự uốn của đồ thị hàm số cho phép chúng ta xác định các điểm uốn và không yêu cầu tồn tại đạo hàm bậc hai tại chúng. Vì vậy, điều kiện đủ thứ nhất có thể coi là phổ quát và được sử dụng nhiều nhất.
Bây giờ chúng ta sẽ xây dựng thêm hai điều kiện đủ cho sự uốn, nhưng chúng chỉ có thể áp dụng được nếu có đạo hàm hữu hạn tại điểm uốn theo một bậc nhất định.
Điều kiện đủ thứ hai để uốn.
Nếu , a , thì hoành độ của điểm uốn của đồ thị hàm số y=f(x) x=3 khác 0. 
Rõ ràng, giá trị của đạo hàm bậc ba khác 0 với mọi x, kể cả x=3. Do đó, theo điều kiện đủ thứ hai cho độ uốn của đồ thị hàm số thì điểm là điểm uốn.
Minh họa đồ họa.
Điều kiện đủ thứ ba để uốn.
Giả sử , a , thì nếu n là số chẵn thì nó là hoành độ của điểm uốn của đồ thị hàm số y=f(x).
Ví dụ.
Tìm điểm uốn của đồ thị hàm số 
.
Giải pháp.
Hàm được xác định trên toàn bộ tập số thực.
Hãy tìm đạo hàm của nó: 
. Rõ ràng, nó cũng được xác định với mọi x thực, do đó, tại bất kỳ điểm nào trên đồ thị của nó đều có một tiếp tuyến không thẳng đứng.
Hãy xác định các giá trị của x mà tại đó đạo hàm bậc hai bằng 0. 
Do đó, tại điểm có trục hoành x=3 có thể có một điểm uốn trên đồ thị của hàm số. Để chắc chắn rằng x = 3 thực sự là hoành độ của điểm uốn, chúng ta sử dụng điều kiện đủ thứ ba. 
Theo điều kiện đủ thứ ba cho sự uốn của đồ thị hàm số, ta có n=4 (đạo hàm bậc năm tiến về 0) - chẵn, do đó x=3 là hoành độ của điểm uốn và điểm của đồ thị hàm số hàm (3;1) tương ứng với nó.
Minh họa đồ họa.
Phần đồ thị hàm số trên khoảng lồi được thể hiện bằng màu xanh lam, trên khoảng lõm – màu đỏ, điểm uốn được thể hiện bằng một chấm đen.
Vẫn còn phải xem xét độ lồi, độ lõm và độ gấp khúc của đồ thị. Hãy bắt đầu với các bài tập thể chất mà khách truy cập trang web vô cùng yêu thích. Hãy đứng lên và nghiêng về phía trước hoặc phía sau. Đây là một chỗ phình ra. Bây giờ bạn hãy dang hai tay ra trước mặt, lòng bàn tay hướng lên trên và tưởng tượng rằng bạn đang ôm một khúc gỗ lớn trước ngực... ...à, nếu bạn không thích khúc gỗ, hãy để việc gì đó/người khác làm việc đó = ) Đây là tính lõm. Một số nguồn có chứa các thuật ngữ đồng nghĩa phồng lên Và phình xuống, nhưng tôi là người thích những tựa đề ngắn.
! Chú ý
: một số tác giả xác định độ lồi và độ lõm hoàn toàn ngược lại. Điều này cũng đúng về mặt toán học và logic, nhưng thường hoàn toàn không chính xác xét theo quan điểm thực chất, kể cả ở mức độ hiểu biết của người bình thường về các thuật ngữ. Vì vậy, ví dụ, một thấu kính có củ được gọi là thấu kính hai mặt lồi, nhưng không có phần lõm (hai mặt lõm).
Và, giả sử, một chiếc giường "lõm" - rõ ràng nó vẫn không "dính" =) (tuy nhiên, nếu bạn trèo xuống dưới nó, thì chúng ta sẽ nói về độ lồi; =)) Tôi tuân theo một cách tiếp cận tương ứng với tự nhiên các hiệp hội của con người.
Định nghĩa chính thức về độ lồi và độ lõm của đồ thị khá khó đối với một ấm trà, vì vậy chúng tôi sẽ giới hạn bản thân trong việc giải thích hình học của khái niệm này bằng các ví dụ cụ thể. Xét đồ thị của hàm số tiếp diễn trên trục số: 
Thật dễ dàng để xây dựng với các phép biến đổi hình học, và có lẽ nhiều độc giả biết làm thế nào nó có được từ một parabol bậc ba.
Hãy gọi dây nhauđường kết nối hai điểm khác nhau nghệ thuật đồ họa.
Đồ thị của hàm số là lồi trên một khoảng nào đó, nếu nó nằm không ít hơn bất kỳ hợp âm nào của một quãng nhất định. Đường thử nghiệm lồi trên , và rõ ràng ở đây bất kỳ phần nào của đồ thị đều nằm TRÊN nó dây nhau. Để minh họa định nghĩa, tôi vẽ ba đường màu đen.
Các hàm đồ thị là lõm trên khoảng, nếu nó nằm không cao hơn bất kỳ hợp âm nào của quãng này. Trong ví dụ đang được xem xét, bệnh nhân bị lõm ở khoảng cách đó. Một cặp đoạn màu nâu chứng minh một cách thuyết phục rằng ở đây bất kỳ phần nào của biểu đồ đều nằm DƯỚI nó dây nhau.
Điểm trên đồ thị mà tại đó nó thay đổi từ lồi sang lõm hoặc từ lõm đến lồi được gọi là điểm uốn. Chúng ta có nó trong một bản sao duy nhất (trường hợp đầu tiên) và trong thực tế, theo điểm uốn, chúng ta có thể hiểu cả điểm xanh thuộc về chính đường đó và giá trị “X”.
QUAN TRỌNG! Các đường gấp khúc của đồ thị phải được vẽ cẩn thận và rất mịn. Tất cả các loại “bất thường” và “thô bạo” đều không thể chấp nhận được. Nó chỉ cần một chút đào tạo.
Cách tiếp cận thứ hai để xác định độ lồi/lõm trong lý thuyết được đưa ra thông qua các tiếp tuyến:
lồi trên khoảng đồ thị nằm không cao hơn tiếp tuyến với nó tại một điểm tùy ý trong một khoảng cho trước. Lõm trên biểu đồ khoảng – không ít hơn bất kỳ tiếp tuyến nào trên khoảng này.
Hyperbol lõm trên khoảng và lồi trên: 
Khi đi qua gốc tọa độ thì độ lõm chuyển thành lồi nhưng điểm KHÔNG ĐẾMđiểm uốn, vì hàm không xác định trong đó.
Bạn có thể tìm thấy các tuyên bố và định lý chặt chẽ hơn về chủ đề này trong sách giáo khoa và chúng ta chuyển sang phần thực hành chuyên sâu:
Cách tìm khoảng lồi, khoảng lõm
và điểm uốn của đồ thị?
Vật liệu đơn giản, có khuôn mẫu và lặp lại cấu trúc nghiên cứu hàm số cực trị.
Độ lồi/lõm của đồ thị đặc trưng Dẫn xuất thứ hai chức năng.
Giả sử hàm khả vi hai lần trên một khoảng nào đó. Sau đó:
– nếu đạo hàm bậc hai nằm trên một khoảng thì đồ thị của hàm số lồi trên khoảng này;
– nếu đạo hàm bậc hai nằm trên một khoảng thì đồ thị của hàm số lõm trên khoảng này.
Về dấu hiệu của đạo hàm bậc hai, một hiệp hội thời tiền sử đang dạo quanh các cơ sở giáo dục: “–” chứng tỏ “bạn không thể đổ nước vào đồ thị của hàm số” (lồi),
và “+” – “mang lại cơ hội như vậy” (độ lõm).
Điều kiện uốn cần thiết
Nếu tại một điểm có một điểm uốn trong đồ thị hàm số, Cái đó:
hoặc giá trị không tồn tại(hãy sắp xếp nó ra, đọc!).
Cụm từ này ngụ ý rằng chức năng tiếp diễn tại một điểm và trong trường hợp – khả vi hai lần trong một lân cận nào đó của nó.
Sự cần thiết của điều kiện cho thấy điều ngược lại không phải lúc nào cũng đúng. Nghĩa là, từ sự bình đẳng (hoặc không tồn tại giá trị) chưa nên sự tồn tại của một điểm uốn trong đồ thị của hàm số tại điểm . Nhưng trong cả hai tình huống họ đều gọi điểm tới hạn của đạo hàm bậc hai.
Điều kiện đủ để uốn
Nếu đạo hàm bậc hai đổi dấu khi đi qua một điểm thì tại thời điểm này đồ thị của hàm số có một điểm uốn.
Có thể không có điểm uốn nào cả (một ví dụ đã được đáp ứng) và theo nghĩa này, một số ví dụ cơ bản chỉ mang tính biểu thị. Hãy phân tích đạo hàm bậc hai của hàm số: 
Ta thu được một hàm hằng dương, đó là với bất kỳ giá trị nào của "x". Sự thật nằm trên bề mặt: parabol lõm toàn bộ miền định nghĩa, không có điểm uốn. Dễ dàng nhận thấy rằng hệ số âm khi “đảo ngược” parabol và làm cho nó lồi (như đạo hàm bậc hai, một hàm hằng số âm, sẽ cho chúng ta biết).
Hàm số mũ cũng lõm tại: 
với bất kỳ giá trị nào của "x".
Tất nhiên đồ thị không có điểm uốn.
Chúng ta xét đồ thị của hàm logarit về độ lồi/lõm:
Do đó, nhánh của logarit là lồi trên khoảng. Đạo hàm bậc hai cũng được xác định trên khoảng, nhưng hãy xem xét nó NÓ BỊ CẤM, vì khoảng này không được bao gồm trong lãnh địa chức năng Yêu cầu là hiển nhiên - vì không có biểu đồ logarit ở đó, nên tất nhiên không có cuộc nói chuyện nào về bất kỳ độ lồi/lõm/uốn cong nào.
Như bạn có thể thấy, mọi thứ thực sự rất gợi nhớ đến câu chuyện với tăng, giảm và cực trị của hàm số. Giống mình thuật toán nghiên cứu đồ thị của hàm sốvề độ lồi, độ lõm và sự hiện diện của các đường gấp khúc:
2) Chúng tôi đang tìm kiếm các giá trị quan trọng. Để làm điều này, hãy lấy đạo hàm bậc hai và giải phương trình. Các điểm tại đó không có đạo hàm bậc 2 nhưng nằm trong miền định nghĩa của chính hàm số cũng được coi là tới hạn!
3) Đánh dấu trên trục số tất cả các điểm dừng và điểm tới hạn tìm được ( có thể không có cái này hay cái kia - thì không cần phải vẽ bất cứ thứ gì (như trong trường hợp quá đơn giản), chỉ cần giới hạn bản thân trong một bình luận bằng văn bản là đủ). Phương pháp ngắt quãng xác định các dấu hiệu trên các khoảng kết quả. Như vừa giải thích, người ta nên xem xét chỉ có những người các khoảng thuộc miền định nghĩa của hàm số. Chúng tôi rút ra kết luận về độ lồi/lõm và điểm uốn của đồ thị hàm số. Chúng tôi đưa ra câu trả lời.
Cố gắng áp dụng bằng lời thuật toán cho các hàm 
. Nhân tiện, trong trường hợp thứ hai, có một ví dụ khi không có điểm uốn trong biểu đồ tại điểm tới hạn. Tuy nhiên, hãy bắt đầu với những nhiệm vụ khó hơn một chút:
ví dụ 1
Giải pháp:
1) Hàm số xác định và liên tục trên trục số. Rất tốt.
2) Hãy tìm đạo hàm bậc hai. Trước tiên, bạn có thể thực hiện việc xây dựng khối lập phương, nhưng việc sử dụng nó sẽ mang lại nhiều lợi nhuận hơn quy tắc lấy vi phân của hàm phức:
Xin lưu ý rằng 
, có nghĩa là hàm này không giảm. Mặc dù điều này không liên quan đến nhiệm vụ nhưng bạn nên luôn chú ý đến những sự thật như vậy.
Hãy tìm các điểm tới hạn của đạo hàm bậc hai:
- Điểm cốt lõi
3) Kiểm tra xem điều kiện uốn đủ có thỏa mãn hay không. Chúng ta hãy xác định dấu của đạo hàm bậc hai trên các khoảng kết quả.
Chú ý! Bây giờ chúng ta đang làm việc với đạo hàm cấp hai (không phải với hàm!)
Kết quả là đạt được một điểm tới hạn: .
3) Đánh dấu hai điểm gián đoạn trên trục số, một điểm tới hạn và xác định dấu của đạo hàm bậc hai trên các khoảng thu được:
Tôi nhắc nhở bạn về một kỹ thuật quan trọng phương pháp khoảng, cho phép bạn tăng tốc đáng kể giải pháp. Dẫn xuất thứ hai 
hóa ra rất cồng kềnh, vì vậy không cần thiết phải tính toán các giá trị của nó, chỉ cần đưa ra “ước tính” ở mỗi khoảng là đủ. Ví dụ, chúng ta hãy chọn một điểm thuộc khoảng bên trái,
và thực hiện thay thế: 
Bây giờ hãy phân tích các số nhân: 
Do đó, hai “trừ” và “cộng” sẽ cho ra “cộng”, có nghĩa là đạo hàm bậc hai dương trong toàn bộ khoảng.
Các hành động nhận xét rất dễ thực hiện bằng lời nói. Ngoài ra, sẽ có lợi nếu bỏ qua yếu tố này hoàn toàn - nó dương với bất kỳ chữ “x” nào và không ảnh hưởng đến dấu của đạo hàm bậc hai của chúng ta.
Vậy bạn đã cung cấp thông tin gì cho chúng tôi?
Trả lời: Đồ thị của hàm số lõm tại 
và lồi trên 
. Tại nguồn gốc (Rõ ràng là ) có một điểm uốn trong đồ thị.
Khi đi qua các điểm, đạo hàm bậc hai cũng đổi dấu, nhưng chúng không được coi là điểm uốn vì hàm số chịu ảnh hưởng của chúng. nghỉ giải lao bất tận.
Trong ví dụ được phân tích, đạo hàm bậc nhất 
thông báo cho chúng tôi về sự phát triển của chức năng trong suốt miền định nghĩa. Sẽ luôn có một món quà miễn phí như vậy =) Ngoài ra, rõ ràng là có ba đường tiệm cận. Đã thu được rất nhiều dữ liệu, cho phép chúng tôi trình bày diện mạo của biểu đồ với độ tin cậy cao. Đối với heap, hàm này cũng lẻ. Dựa trên các dữ kiện đã được thiết lập, hãy cố gắng tạo ra một bản phác thảo thô. Hình ảnh ở cuối bài học.
Nhiệm vụ cho giải pháp độc lập:
Ví dụ 6
Xét tính lồi, lõm của đồ thị hàm số và tìm các điểm uốn của đồ thị nếu có.
Mẫu không có hình vẽ nhưng không cấm đưa ra giả thuyết ;)
Chúng tôi nghiền vật liệu mà không đánh số các điểm của thuật toán:
Ví dụ 7
Xét đồ thị của hàm số về độ lồi, độ lõm và tìm các điểm uốn nếu chúng tồn tại.
Giải pháp: chức năng chịu đựng khoảng cách vô tậnỞ điểm .
Như thường lệ, mọi thứ đều ổn với chúng tôi: 
Công cụ phái sinh không phải là khó nhất, cái chính là phải cẩn thận với “kiểu tóc” của mình.
Trong cuộc chạy marathon cảm ứng, hai điểm tới hạn của đạo hàm bậc hai được bộc lộ: 
Hãy để chúng tôi xác định các dấu hiệu trên các khoảng kết quả:
Có một điểm uốn trong đồ thị tại một điểm; 
Khi đi qua một điểm đạo hàm bậc hai không đổi dấu nên đồ thị KHÔNG có điểm uốn.
Trả lời: khoảng lồi: 
; khoảng lõm: ; điểm uốn: .
Hãy xem các ví dụ cuối cùng với chuông và còi bổ sung:
Ví dụ 8
Tìm các khoảng lồi, lõm và các điểm uốn của đồ thị
Giải pháp: với việc tìm kiếm miền định nghĩa Không có vấn đề đặc biệt:
, trong khi hàm số bị gián đoạn tại các điểm.
Chúng ta hãy đi theo con đường bị đánh đập: 
- Điểm cốt lõi.
Hãy xác định các dấu hiệu và xem xét các khoảng chỉ từ miền chức năng:
Có một điểm uốn trong đồ thị tại một điểm; hãy tính tọa độ: 
