График на функција со дробна моќ. Функција. Функција за напојување
На оваа лекцијаќе го продолжиме нашето проучување на функциите на моќта со рационален индикатор, разгледајте ги функциите со негативен рационален експонент.
1. Основни поими и дефиниции
Да се потсетиме на својствата и графиконите на функциите на моќност со негативен цел број експонент.
За дури n,:
Пример функција:
Сите графикони на таквите функции минуваат низ две фиксни точки: (1;1), (-1;1). Особеноста на функциите од овој тип е нивната паритет, графиконите се симетрични во однос на оската оп-засилувач.

Ориз. 1. График на функција
За непарни n,:
Пример функција:
Сите графикони на таквите функции минуваат низ две фиксни точки: (1;1), (-1;-1). Особеноста на функциите од овој тип е тоа што тие се непарни, графиконите се симетрични во однос на потеклото.

Ориз. 2. График на функција
2. Функција со негативен рационален експонент, графикони, својства
Да се потсетиме на основната дефиниција.
Моќта на ненегативен број a со рационален позитивен експонент се нарекува број.
Степен позитивен броја со рационален негативен експонент се нарекува број.
За еднаквост:
![]()
![]()
На пример: ![]() ; - изразот не постои, по дефиниција, за степен со негативен рационален експонент; постои затоа што експонентот е цел број,
; - изразот не постои, по дефиниција, за степен со негативен рационален експонент; постои затоа што експонентот е цел број, ![]()
Ајде да продолжиме со разгледување на функциите на моќност со рационален негативен експонент.
![]()
На пример:
За да нацртате график на оваа функција, можете да креирате табела. Ќе го направиме тоа поинаку: прво ќе го изградиме и проучуваме графикот на именителот - ни е познат (Слика 3).

Ориз. 3. График на функција
Графикот на функцијата именител поминува низ фиксна точка (1;1). При исцртување на оригиналната функција дадена точкаостанува, кога коренот исто така се стреми кон нула, функцијата се стреми кон бесконечност. И, обратно, како што x се стреми кон бесконечност, функцијата се стреми кон нула (Слика 4).

Ориз. 4. График на функции
Да разгледаме уште една функција од семејството на функции што се проучуваат.
![]()
Важно е дека по дефиниција
Да го разгледаме графикот на функцијата во именителот: , графикот на оваа функција ни е познат, тој се зголемува во својот домен на дефиниција и поминува низ точката (1;1) (слика 5).

Ориз. 5. График на функција
При исцртување на графикот на првобитната функција, точката (1;1) останува, додека коренот исто така се стреми кон нула, функцијата се стреми кон бесконечност. И, обратно, како што x се стреми кон бесконечност, функцијата се стреми кон нула (Слика 6).

Ориз. 6. График на функција
Разгледаните примери помагаат да се разбере како тече графикот и кои се својствата на функцијата што се проучува - функција со негативен рационален експонент.
Графиконите на функции од оваа фамилија минуваат низ точката (1;1), функцијата се намалува низ целиот домен на дефиниција.
Опсег на функција: ![]()
Функцијата не е ограничена одозгора, туку е ограничена одоздола. Функцијата нема ниту најголем ниту најниска вредност.
Функцијата е континуирана, прифаќа сè позитивни вредностиод нула до плус бесконечност.
Функцијата е конвексна надолу (Слика 15.7)
Точките А и Б се земаат на кривата, низ нив се повлекува отсечка, целата крива е под отсечката, овој услов е задоволен за произволни две точки на кривата, затоа функцијата е конвексна надолу. Ориз. 7.

Ориз. 7. Конвексност на функцијата
3. Решавање на типични проблеми
Важно е да се разбере дека функциите на ова семејство се ограничени одоздола со нула, но немаат најмала вредност.
Пример 1 - најдете го максимумот и минимумот на функцијата на интервалот \[(\mathop(lim)_(x\to +\infty ) x^(2n)\ )=+\infty \]
Графикон (сл. 2).

Слика 2. График на функцијата $f\left(x\right)=x^(2n)$
Својства на функција на моќност со природен непарен експонент
Доменот на дефиниција се сите реални броеви.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- функцијата е непарна.
$f(x)$ е континуиран во целиот домен на дефиниција.
Опсегот е сите реални броеви.
$f"\лево(x\десно)=\лево(x^(2n-1)\десно)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Функцијата се зголемува во целиот домен на дефиниција.
$f\left(x\десно)0$, за $x\in (0,+\infty)$.
$f (""\лево(x\десно))=(\лево(\лево(2n-1\десно)\cdot x^(2\лево(n-1\десно))\десно)"=2 \лево(2n-1\десно)(n-1)\cточка x^(2n-3)$
\ \
Функцијата е конкавна за $x\in (-\infty ,0)$ и конвексна за $x\in (0,+\infty)$.
Графикон (сл. 3).
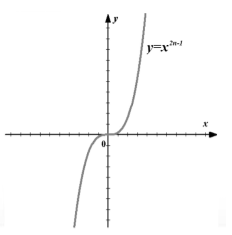
Слика 3. График на функцијата $f\left(x\right)=x^(2n-1)$
Функција на моќност со цел број експонент
Прво, да го воведеме концептот на степен со цел број експонент.
Дефиниција 3
Моќта на реален број $a$ со цел број на експонент $n$ се одредува со формулата:

Слика 4.
Сега да разгледаме функција на моќност со цел број експонент, нејзините својства и графикон.
Дефиниција 4
$f\left(x\right)=x^n$ ($n\in Z)$ се нарекува функција на моќност со цел број експонент.
Ако степенот е поголем од нула, тогаш доаѓаме до случај на функција на моќност со природен индикатор. Веќе разговаравме погоре. За $n=0$ добиваме линеарна функција$y=1$. Неговото разгледување ќе го оставиме на читателот. Останува да се разгледаат својствата на функцијата моќност со негативен цел број експонент
Својства на функцијата моќност со негативен цел број експонент
Доменот на дефиниција е $\left(-\infty ,0\right)(0,+\infty)$.
Ако експонентот е парен, тогаш функцијата е парна ако е непарна, тогаш функцијата е непарна.
$f(x)$ е континуиран во целиот домен на дефиниција.
Опсег:
Ако експонентот е парен, тогаш $(0,+\infty)$ ако е непарен, тогаш $\left(-\infty ,0\right)(0,+\infty)$;
За непарен експонент, функцијата се намалува како $x\in \left(-\infty ,0\right)(0,+\infty)$. Ако експонентот е парен, функцијата се намалува како $x\in (0,+\infty)$. и се зголемува како $x\in \left(-\infty,0\right)$.
$f(x)\ge 0$ во целиот домен на дефиниција
За погодност да се разгледа функцијата на моќност, ќе разгледаме 4 посебни случаи: функција на моќност со природен експонент, функција на моќност со цел број експонент, функција на моќност со рационален експонент и функција на моќност со ирационален експонент.
Функција на моќност со природен експонент
Прво, да го воведеме концептот на диплома со природен експонент.
Дефиниција 1
Моќта на реален број $a$ со природен експонент $n$ е број еднаков на производот од $n$ фактори, од кои секој е еднаков на бројот $a$.
Слика 1.
$a$ е основа на степенот.
$n$ е експонентот.
Сега да разгледаме функција на моќност со природен експонент, нејзините својства и графикон.
Дефиниција 2
$f\left(x\right)=x^n$ ($n\in N)$ се нарекува функција на моќност со природен експонент.
За понатамошна погодност, одделно разгледуваме функција на моќност со парен експонент $f\left(x\right)=x^(2n)$ и функција за моќност со непарен експонент $f\left(x\right)=x^ (2n-1)$ ($n\во N)$.
Својства на функција на моќност со природен парен експонент
$f\left(-x\right)=((-x))^(2n)=x^(2n)=f(x)$ -- функцијата е парна.
Област на вредност -- $\
Функцијата се намалува како $x\in (-\infty ,0)$ и се зголемува како $x\in (0,+\infty)$.
$f("")\лево(x\десно)=(\лево(2n\cточка x^(2n-1)\десно))"=2n(2n-1)\cточка x^(2(n-1 ))\ge 0$
Функцијата е конвексна во целиот домен на дефиниција.
Однесување на краевите на доменот:
\[(\mathop(lim)_(x\to -\infty) x^(2n)\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty) x^( 2n)\ )=+\infty \]
Графикон (сл. 2).

Слика 2. График на функцијата $f\left(x\right)=x^(2n)$
Својства на функција на моќност со природен непарен експонент
Доменот на дефиниција се сите реални броеви.
$f\left(-x\right)=((-x))^(2n-1)=(-x)^(2n)=-f(x)$ -- функцијата е непарна.
$f(x)$ е континуиран во целиот домен на дефиниција.
Опсегот е сите реални броеви.
$f"\лево(x\десно)=\лево(x^(2n-1)\десно)"=(2n-1)\cdot x^(2(n-1))\ge 0$
Функцијата се зголемува во целиот домен на дефиниција.
$f\left(x\десно)0$, за $x\in (0,+\infty)$.
$f (""\лево(x\десно))=(\лево(\лево(2n-1\десно)\cdot x^(2\лево(n-1\десно))\десно)"=2 \лево(2n-1\десно)(n-1)\cточка x^(2n-3)$
\ \
Функцијата е конкавна за $x\in (-\infty ,0)$ и конвексна за $x\in (0,+\infty)$.
Графикон (сл. 3).

Слика 3. График на функцијата $f\left(x\right)=x^(2n-1)$
Функција на моќност со цел број експонент
Прво, да го воведеме концептот на степен со цел број експонент.
Дефиниција 3
Моќта на реален број $a$ со цел број на експонент $n$ се одредува со формулата:

Слика 4.
Сега да разгледаме функција на моќност со цел број експонент, нејзините својства и графикон.
Дефиниција 4
$f\left(x\right)=x^n$ ($n\in Z)$ се нарекува функција на моќност со цел број експонент.
Ако степенот е поголем од нула, тогаш доаѓаме до случај на функција на моќност со природен експонент. Веќе разговаравме погоре. За $n=0$ добиваме линеарна функција $y=1$. Неговото разгледување ќе го оставиме на читателот. Останува да се разгледаат својствата на функцијата на моќност со негативен цел број експонент
Својства на функцијата моќност со негативен цел број експонент
Доменот на дефиниција е $\left(-\infty ,0\right)(0,+\infty)$.
Ако експонентот е парен, тогаш функцијата е парна ако е непарна, тогаш функцијата е непарна.
$f(x)$ е континуиран во целиот домен на дефиниција.
Опсег:
Ако експонентот е парен, тогаш $(0,+\infty)$ ако е непарен, тогаш $\left(-\infty ,0\right)(0,+\infty)$;
За непарен експонент, функцијата се намалува како $x\in \left(-\infty ,0\right)(0,+\infty)$. Ако експонентот е парен, функцијата се намалува како $x\in (0,+\infty)$. и се зголемува како $x\in \left(-\infty,0\right)$.
$f(x)\ge 0$ во целиот домен на дефиниција

